
【题目】设函数f(x)=loga(1+![]() x),g(x)=loga(1-
x),g(x)=loga(1-![]() x),(a>0且a≠1),若h(x)=f(x)-g(x).
x),(a>0且a≠1),若h(x)=f(x)-g(x).
(1)求函数h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若f(2)=1,求使h(x)>0成立的x的集合.
【答案】(1)(-2,2)
(2) h(x)为奇函数
(3) ![]()
【解析】
(1)根据函数定义域的定义,列出使得![]() 有意义的条件,即可求解函数的定义域;
有意义的条件,即可求解函数的定义域;
(2)根据函数的奇偶性性的定义,即可作出证明,得到函数![]() 的奇偶性;
的奇偶性;
(3)由![]() ,求得
,求得![]() ,得到函数
,得到函数![]() 的解析式,再由
的解析式,再由![]() ,得到不等式
,得到不等式![]() ,即可求得不等式的解集.
,即可求得不等式的解集.
(1)由1+![]() x>0且1-
x>0且1-![]() x>0得-2<x<2,所以函数定义域为(-2,2)
x>0得-2<x<2,所以函数定义域为(-2,2)
(2)∵对任意的x∈(-2,2),-x∈(-2,2),
![]()
所以h(x)为奇函数
(3) f(2)=1,得a=2.此时h(x)=log2(1+![]() x)-log2(1-
x)-log2(1-![]() x),
x),
由h(x)>0得:1+![]() x>1-
x>1-![]() x,所以x>0
x,所以x>0
又由(1)知 -2<x<2所以0<x<2,![]() x的取值集合为
x的取值集合为![]()


科目:高中数学 来源: 题型:
【题目】(选修4﹣4:坐标系与参数方程)
已知曲线C1的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调区间和极值.
的单调区间和极值.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)根据导数几何意义得![]() ,再与
,再与![]() 联立方程组解得
联立方程组解得![]() ,
, ![]() (2)先函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值
(2)先函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值
试题解析:(1)![]() ,切线为
,切线为![]() ,即斜率
,即斜率![]() ,纵坐标
,纵坐标![]()
即![]() ,
, ![]() ,解得
,解得![]() ,
, ![]()
解析式![]()
(2)![]()
![]()
![]() ,定义域为
,定义域为![]()
得到![]() 在
在![]() 单增,在
单增,在![]() 单减,在
单减,在![]() 单增
单增
极大值![]() ,极小值
,极小值![]() .
.
【题型】解答题
【结束】
20
【题目】如图:在四棱锥![]() 中,底面
中,底面![]() 为菱形,且
为菱形,且![]() ,
, ![]() 底面
底面![]() ,
,
![]() ,
, ![]() ,
, ![]() 是
是![]() 上点,且
上点,且![]() 平面
平面![]() .
.
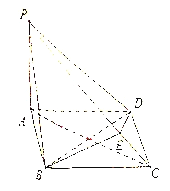
(1)求证: ![]() ;(2)求三棱锥
;(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在框图中,设x=2,并在输入框中输入n=4;ai=i(i=0,1,2,3,4).则此程序执行后输出的S值为( ) 
A.26
B.49
C.52
D.98
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :若关于
:若关于![]() 的方程
的方程![]() 无实数根,则
无实数根,则![]() ;命题
;命题![]() :若关于
:若关于![]() 的方程
的方程![]() 有两个不相等的正实数根,则
有两个不相等的正实数根,则![]() .
.
(1)写出命题![]() 的否命题,并判断命题
的否命题,并判断命题![]() 的真假;
的真假;
(2)判断命题“![]() 且
且![]() ”的真假,并说明理由.
”的真假,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的两个焦点分别为
的两个焦点分别为![]() ,
, ![]() ,且点
,且点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于异于
相交于异于![]() 的不同两点
的不同两点![]() ,求
,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在![]() 年的自主招生考试成绩中随机抽取
年的自主招生考试成绩中随机抽取![]() 名学生的笔试成绩,按成绩分组:第
名学生的笔试成绩,按成绩分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() 得到的频率分布直方图如图所示.
得到的频率分布直方图如图所示.

(1)分别求第![]() ,
, ![]() ,
, ![]() 组的频率;
组的频率;
(2)若该校决定在笔试成绩高的第![]() ,
, ![]() ,
, ![]() 组中用分层抽样抽取
组中用分层抽样抽取![]() 名学生进入第二轮面试,求第
名学生进入第二轮面试,求第![]() ,
, ![]() ,
, ![]() 组每组各抽取多少名学生进入第二轮面试?
组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受甲考官的面试,求第
名学生接受甲考官的面试,求第![]() 组至少有一名学生被甲考官面试的概率.
组至少有一名学生被甲考官面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
时间x | 1 | 2 | 3 | 4 | 5 |
命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
小李这5天的平均投篮命中率为 ;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com