
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏΖΫ≥ΧΈΣ
¥ΠΒΡ«–œΏΖΫ≥ΧΈΣ![]() .
.
Θ®1Θ©«σΚ· ΐ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
Θ®2Θ©«σΚ· ΐ![]() ΒΡΒΞΒς«χΦδΚΆΦΪ÷Β.
ΒΡΒΞΒς«χΦδΚΆΦΪ÷Β.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ;Θ®2Θ©ΦϊΫβΈω.
;Θ®2Θ©ΦϊΫβΈω.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΒΦ ΐΦΗΚΈ“β“εΒΟ![]() Θ§‘Ό”κ
Θ§‘Ό”κ![]() ΝΣΝΔΖΫ≥ΧΉιΫβΒΟ
ΝΣΝΔΖΫ≥ΧΉιΫβΒΟ![]() Θ§
Θ§ ![]() Θ®2Θ©œ»Κ· ΐΒΦ ΐ,‘Ό«σΒΦΚ· ΐΝψΒψ,Ν–±μΖ÷ΈωΒΦΚ· ΐΖϊΚ≈±δΜ·Ιφ¬…,ΫχΕχ»ΖΕ®ΒΞΒς«χΦδΚΆΦΪ÷Β
Θ®2Θ©œ»Κ· ΐΒΦ ΐ,‘Ό«σΒΦΚ· ΐΝψΒψ,Ν–±μΖ÷ΈωΒΦΚ· ΐΖϊΚ≈±δΜ·Ιφ¬…,ΫχΕχ»ΖΕ®ΒΞΒς«χΦδΚΆΦΪ÷Β
‘ΧβΫβΈωΘΚΘ®1Θ©![]() Θ§«–œΏΈΣ
Θ§«–œΏΈΣ![]() Θ§Φ¥–±¬
Θ§Φ¥–±¬ ![]() Θ§ΉίΉχ±ξ
Θ§ΉίΉχ±ξ![]()
Φ¥![]() Θ§
Θ§ ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§ ![]()
ΫβΈω Ϋ![]()
Θ®2Θ©![]()
![]()
![]() Θ§Ε®“ε”ρΈΣ
Θ§Ε®“ε”ρΈΣ![]()
ΒΟΒΫ![]() ‘Ύ
‘Ύ![]() ΒΞ‘ωΘ§‘Ύ
ΒΞ‘ωΘ§‘Ύ![]() ΒΞΦθΘ§‘Ύ
ΒΞΦθΘ§‘Ύ![]() ΒΞ‘ω
ΒΞ‘ω
ΦΪ¥σ÷Β![]() Θ§ΦΪ–Γ÷Β
Θ§ΦΪ–Γ÷Β![]() .
.
ΓΨΧβ–ΆΓΩΫβ¥πΧβ
ΓΨΫα χΓΩ
20
ΓΨΧβΡΩΓΩ»γΆΦΘΚ‘ΎΥΡάβΉΕ![]() ÷–Θ§ΒΉΟφ
÷–Θ§ΒΉΟφ![]() ΈΣΝβ–ΈΘ§«“
ΈΣΝβ–ΈΘ§«“![]() Θ§
Θ§ ![]() ΒΉΟφ
ΒΉΟφ![]() Θ§
Θ§
![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() «
«![]() …œΒψΘ§«“
…œΒψΘ§«“![]() ΤΫΟφ
ΤΫΟφ![]() .
.
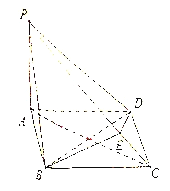
Θ®1Θ©«σ÷ΛΘΚ ![]() ΘΜΘ®2Θ©«σ»ΐάβΉΕ
ΘΜΘ®2Θ©«σ»ΐάβΉΕ![]() ΒΡΧεΜΐ.
ΒΡΧεΜΐ.

| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τ Β ΐxΓΔyΓΔm¬ζΉψ|x©¹m|ΘΦ|y©¹m|Θ§‘ρ≥Τx±»yΫ”ΫϋmΘ°
Θ®1Θ©»τ2x±»1Ϋ”Ϋϋ3Θ§«σxΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©“―÷ΣΚ· ΐfΘ®xΘ©Ε®“ε”ρD=Θ®©¹ΓόΘ§0Θ©Γ»Θ®0Θ§1Θ©Γ»Θ®1Θ§3Θ©Γ»Θ®3Θ§+ΓόΘ©Θ§Ε‘”Ύ»Έ“βΒΡxΓ DΘ§fΘ®xΘ©Β»”Ύx2©¹2x”κx÷–Ϋ”Ϋϋ0ΒΡΡ«Ηω÷ΒΘ§–¥≥ωΚ· ΐfΘ®xΘ©ΒΡΫβΈω ΫΘ§»τΙΊ”ΎxΒΡΖΫ≥ΧfΘ®xΘ©©¹a=0”–ΝΫΗω≤ΜΆ§ΒΡ Β ΐΗυΘ§«σ≥ωaΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©“―÷ΣaΘ§bΓ RΘ§mΘΨ0«“aΓΌbΘ§«σ÷ΛΘΚ ![]() ±»
±» ![]() Ϋ”Ϋϋ0Θ°
Ϋ”Ϋϋ0Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() ΒΡΕ®“ε”ρΈΣ
ΒΡΕ®“ε”ρΈΣ![]() Θ§Ε‘»Έ“β Β ΐ
Θ§Ε‘»Έ“β Β ΐ![]() Θ§ΕΦ”–
Θ§ΕΦ”–![]() Θ°
Θ°
Θ®1Θ©«σ![]() ΒΡ÷Β≤Δ≈–ΕœΚ· ΐ
ΒΡ÷Β≤Δ≈–ΕœΚ· ΐ![]() ΒΡΤφ≈Φ–‘ΘΜ
ΒΡΤφ≈Φ–‘ΘΜ
Θ®2Θ©“―÷ΣΚ· ΐ![]() Θ§
Θ§
ΔΌ―ι÷ΛΚ· ΐ![]() «Ζώ¬ζΉψΧβΗ…÷–ΒΡΧθΦΰΘ§Φ¥―ι÷ΛΕ‘»Έ“β Β ΐ
«Ζώ¬ζΉψΧβΗ…÷–ΒΡΧθΦΰΘ§Φ¥―ι÷ΛΕ‘»Έ“β Β ΐ![]() Θ§
Θ§![]() «Ζώ≥…ΝΔΘΜ
«Ζώ≥…ΝΔΘΜ
ΔΎ»τΚ· ΐ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() Θ§Χ÷¬έΚ· ΐ
Θ§Χ÷¬έΚ· ΐ![]() ΒΡΝψΒψΗω ΐ«ιΩωΘ°
ΒΡΝψΒψΗω ΐ«ιΩωΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τ‘≤CΒΡΑκΨΕΈΣ1Θ§‘≤–Ρ‘ΎΒΎ“ΜœσœόΘ§«“”κ÷±œΏ4x©¹3y=0ΚΆx÷αΕΦœύ«–Θ§‘ρΗΟ‘≤ΒΡ±ξΉΦΖΫ≥Χ «Θ® Θ©
A.Θ®x©¹2Θ©2+Θ®y©¹1Θ©2=1
B.Θ®x©¹2Θ©2+Θ®y+1Θ©2=1
C.Θ®x+2Θ©2+Θ®y©¹1Θ©2=1
D.Θ®x©¹3Θ©2+Θ®y©¹1Θ©2=1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() ΈΣάβ≥Λ
ΈΣάβ≥Λ![]() ΒΡ’ΐΖΫΧεΘ§
ΒΡ’ΐΖΫΧεΘ§ ![]() ΈΣάβ
ΈΣάβ![]() ΒΡ÷–Βψ.
ΒΡ÷–Βψ.
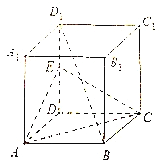
Θ®1Θ©«σ»ΐάβΉΕ![]() ΒΡΧεΜΐΘΜ
ΒΡΧεΜΐΘΜ
Θ®2Θ©«σ÷ΛΘΚ ![]() ΤΫΟφ
ΤΫΟφ![]() .
.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ;Θ®2Θ©ΦϊΫβΈω.
;Θ®2Θ©ΦϊΫβΈω.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗΏΈΣED,‘ΌΗυΨίΉΕΧεΧεΜΐΙΪ ΫΦΤΥψΧεΜΐΘ®2Θ©Ν§Ϋ”![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§ΗυΨί»ΐΫ«–Έ÷–ΈΜœΏ–‘÷ ΒΟ
Θ§ΗυΨί»ΐΫ«–Έ÷–ΈΜœΏ–‘÷ ΒΟ![]() Θ§‘ΌΗυΨίœΏΟφΤΫ––≈–Ε®Ε®άμΒΟΫα¬έ
Θ§‘ΌΗυΨίœΏΟφΤΫ––≈–Ε®Ε®άμΒΟΫα¬έ
‘ΧβΫβΈωΘΚΘ®1Θ©ΧεΜΐ![]()
![]()
Θ®2Θ©Ν§Ϋ”![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§‘ρ
Θ§‘ρ![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΈΜœΏΘ§Φ¥
ΒΡ÷–ΈΜœΏΘ§Φ¥![]() Θ§
Θ§
”÷![]() Οφ
Οφ![]() Θ§
Θ§ ![]() Οφ
Οφ![]() Θ§ΒΟΒΫ
Θ§ΒΟΒΫ![]()
![]() ΤΫΟφ
ΤΫΟφ![]() .
.
ΓΨΧβ–ΆΓΩΫβ¥πΧβ
ΓΨΫα χΓΩ
18
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏ![]() ΘΚ
ΘΚ ![]() ΒΡΫΙΒψ
ΒΡΫΙΒψ![]() ΈΣ‘≤
ΈΣ‘≤![]() ΒΡ‘≤–Ρ.
ΒΡ‘≤–Ρ.
Θ®1Θ©«σ≈ΉΈοœΏ![]() ΒΡ±ξΉΦΖΫ≥ΧΘΜ
ΒΡ±ξΉΦΖΫ≥ΧΘΜ
Θ®2Θ©»τ–±¬ ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() Ιΐ≈ΉΈοœΏΒΡΫΙΒψ
Ιΐ≈ΉΈοœΏΒΡΫΙΒψ![]() ”κ≈ΉΈοœΏœύΫΜ”Ύ
”κ≈ΉΈοœΏœύΫΜ”Ύ![]() ΝΫΒψΘ§«σœ“≥Λ
ΝΫΒψΘ§«σœ“≥Λ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘≤CΘΚx2+y2+2x©¹4y+3=0Θ°
Θ®1Θ©»τ‘≤CΒΡ«–œΏ‘Ύx÷αΚΆy÷α…œΒΡΫΊΨύœύΒ»Θ§«σ¥Υ«–œΏΒΡΖΫ≥ΧΘΜ
Θ®2Θ©¥”‘≤CΆβ“ΜΒψPΘ®x1 Θ§ y1Θ©œρΗΟ‘≤“ΐ“ΜΧθ«–œΏΘ§«–ΒψΈΣMΘ§OΈΣΉχ±ξ‘≠ΒψΘ§«“”–|PM|=|PO|Θ§«σ ΙΒΟ|PM|»ΓΒΟΉν–Γ÷ΒΒΡΒψPΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐf(x)ΘΫloga(1ΘΪ![]() x)Θ§g(x)ΘΫloga(1Θ≠
x)Θ§g(x)ΘΫloga(1Θ≠![]() x)Θ§(a>0«“aΓΌ1)Θ§»τh(x)ΘΫf(x)Θ≠g(x)Θ°
x)Θ§(a>0«“aΓΌ1)Θ§»τh(x)ΘΫf(x)Θ≠g(x)Θ°
(1)«σΚ· ΐh(x)ΒΡΕ®“ε”ρΘΜ
(2)≈–Εœh(x)ΒΡΤφ≈Φ–‘Θ§≤ΔΥΒΟςάμ”…ΘΜ
(3)»τf(2)ΘΫ1Θ§«σ Ιh(x)>0≥…ΝΔΒΡxΒΡΦ·ΚœΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘≤![]() Ψ≠ΙΐΒψ
Ψ≠ΙΐΒψ![]() Θ§
Θ§ ![]() ΚΆ÷±œΏ
ΚΆ÷±œΏ![]() œύ«–.
œύ«–.
Θ®1Θ©«σ‘≤![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©»τ÷±œΏ![]() Ψ≠ΙΐΒψ
Ψ≠ΙΐΒψ![]() Θ§≤Δ«“±Μ‘≤
Θ§≤Δ«“±Μ‘≤![]() ΫΊΒΟΒΡœ“≥ΛΈΣ2Θ§«σ÷±œΏ
ΫΊΒΟΒΡœ“≥ΛΈΣ2Θ§«σ÷±œΏ![]() ΒΡΖΫ≥Χ.
ΒΡΖΫ≥Χ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ÷±»ΐάβ÷υ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§‘ρ“λΟφ÷±œΏ
Θ§‘ρ“λΟφ÷±œΏ![]() ”κ
”κ![]() Υυ≥…Ϋ«ΒΡ”ύœ“÷ΒΈΣΘ® Θ©
Υυ≥…Ϋ«ΒΡ”ύœ“÷ΒΈΣΘ® Θ©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com