【题目】某机构为了解某地区中学生在校月消费情况，随机抽取了 100名中学生进行调查.如图是根据调査的结果绘制的学生在校月消费金额的频率分布直方图.已知三个金额段的学生人数成等差数列，将月消费金额不低于550元的学生称为“高消费群”.

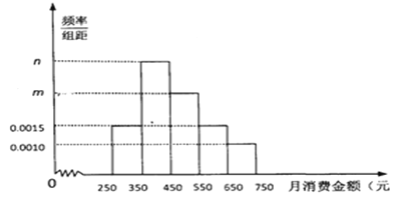
（1）求的值，并求这100名学生月消费金额的样本平均数 (同一组中的数据用该组区间的中点值作代表）；

（2）根据已知条件完成下面列联表，并判断能否有的把握认为“高消费群”与性别有关？

附: (其中样本容量)

【题目】（题文）如图，在多面体中， 是正方形， 平面, 平面, ,点为棱的中点.

（1）求证：平面平面；

（2）若,求三棱锥的体积.

【题目】如图，正方体的棱长为，，是线段上的两个动点，且，则下列结论错误的是 （ ）

A.

B. 直线、所成的角为定值

C. ∥平面

D. 三棱锥的体积为定值

（1）这种“浮球”的体积是多少cm3（结果精确到0.1）?

（2）要在2 500个这样的“浮球”表面涂一层胶，如果每平方米需要涂胶100克，那么共需胶多少克？

【题目】随着电商的快速发展，快递业突飞猛进，到目前，中国拥有世界上最大的快递市场.某快递公司收取快递费的标准是：重量不超过的包裹收费10元；重量超过的包裹，在收费10元的基础上，每超过（不足，按计算）需再收5元.

该公司将最近承揽的100件包裹的重量统计如下：

公司对近60天，每天揽件数量统计如下表：

以上数据已做近似处理，并将频率视为概率.

（1）计算该公司未来5天内恰有2天揽件数在101~300之间的概率；

（2）①估计该公司对每件包裹收取的快递费的平均值；

②根据以往的经验，公司将快递费的三分之一作为前台工作人员的工资和公司利润，其余的用作其他费用.目前前台有工作人员3人，每人每天揽件不超过150件，日工资100元.公司正在考虑是否将前台工作人员裁减1人，试计算裁员前后公司每日利润的数学期望，若你是决策者，是否裁减工作人员1人？

【题目】某学校为了加强学生数学核心素养的培养，锻炼学生自主探究学习的能力，他们以教材第82页第8题的函数为基本素材，研究该函数的相关性质，取得部分研究成果如下：

①同学甲发现：函数的定义域为；

②同学乙发现：函数是偶函数；

③同学丙发现：对于任意的都有；

④同学丁发现：对于任意的，都有；

⑤同学戊发现：对于函数定义域中任意的两个不同实数，总满足.

其中所有正确研究成果的序号是__________．

A. 消耗1升汽油，乙车最多可行驶5千米

B. 以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多

C. 甲车以80千米/小时的速度行驶1小时，消耗10升汽油

D. 某城市机动车最高限速80千米/小时. 相同条件下，在该市用丙车比用乙车更省油

【题目】函数，关于的不等式的解集为.

（Ⅰ）求、的值；

（Ⅱ）设.

（i）若不等式在上恒成立，求实数的取值范围；

（ii）若函数有三个不同的零点，求实数的取值范围（为自然对数的底数）.

【题目】如图，矩形中，，为的中点，现将与折起，使得平面及平面都与平面垂直.

（1）求证：平面；

（2）求二面角的余弦值.

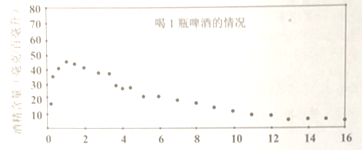
该函数模型如下：

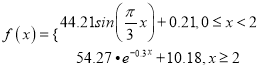
根据上述条件，回答以下问题：

（1）试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值？最大值是多少？

（2）试计算喝1瓶啤酒后多少小时后才可以驾车？（时间以整小时计算）

（参数数据： ， ， ）