
科目: 来源: 题型:
【题目】若函数![]() 具备以下两个条件:(1)至少有一条对称轴或一个对称中心;(2)至少有两个零点,则称这样的函数为“多元素”函数,下列函数中为“多元素”函数的是_______.
具备以下两个条件:(1)至少有一条对称轴或一个对称中心;(2)至少有两个零点,则称这样的函数为“多元素”函数,下列函数中为“多元素”函数的是_______.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中(底面△ABC为正三角形),A1A⊥平面ABC,AB=AC=2,![]() ,D是BC边的中点.
,D是BC边的中点.
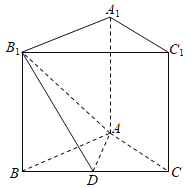
(1)证明:平面ADB1⊥平面BB1C1C.
(2)求点B到平面ADB1的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】某景区的各景点从2009年取消门票实行免费开放后,旅游的人数不断地增加,不仅带动了该市淡季的旅游,而且优化了旅游产业的结构,促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变.下表是从2009年至2018年,该景点的旅游人数![]() (万人)与年份
(万人)与年份![]() 的数据:
的数据:
第 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
旅游人数 | 300 | 283 | 321 | 345 | 372 | 435 | 486 | 527 | 622 | 800 |
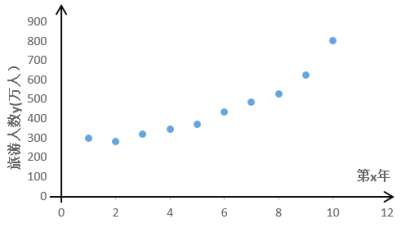
该景点为了预测2021年的旅游人数,建立了![]() 与
与![]() 的两个回归模型:
的两个回归模型:
模型①:由最小二乘法公式求得![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ;
;
模型②:由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近.
的附近.
(1)根据表中数据,求模型②的回归方程![]() .(
.(![]() 精确到个位,
精确到个位,![]() 精确到0.01).
精确到0.01).
(2)根据下列表中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
回归方程 | ① | ② |
| 30407 | 14607 |
参考公式、参考数据及说明:
①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为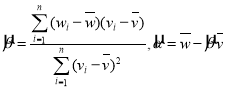 .②刻画回归效果的相关指数
.②刻画回归效果的相关指数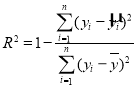 ;③参考数据:
;③参考数据:![]() ,
,![]() .
.
|
|
|
|
|
|
5.5 | 449 | 6.05 | 83 | 4195 | 9.00 |
表中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人进行象棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)用X表示比赛决出胜负时的总局数,求随机变量X的分布列和均值.
查看答案和解析>>
科目: 来源: 题型:
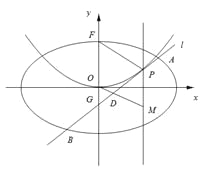
【题目】平面直角坐标系![]() 中,椭圆C:
中,椭圆C:![]() 的离心率是
的离心率是![]() ,抛物线E:
,抛物线E:![]() 的焦点F是C的一个顶点.
的焦点F是C的一个顶点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P是E上的动点,且位于第一象限,E在点P处的切线![]() 与C交与不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
与C交与不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
(ⅰ)求证:点M在定直线上;
(ⅱ)直线![]() 与y轴交于点G,记△
与y轴交于点G,记△![]() 的面积为
的面积为![]() ,△
,△![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值及取得最大值时点P的坐标.
的最大值及取得最大值时点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一平面与空间四边形![]() 的对角线
的对角线![]() ,
,![]() 都平行,且交空间四边形的边
都平行,且交空间四边形的边![]() ,
,![]() ,
,![]() ,
,![]() 分别于
分别于![]() ,
,![]() ,
,![]() ,
,![]() .
.
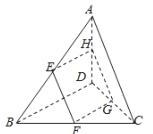
(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)若![]() 是边
是边![]() 的中点,
的中点,![]() ,
,![]() ,异面直线
,异面直线![]() 与
与![]() 所成的角为60°,求线段
所成的角为60°,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】大豆,古称菽,原产中国,在中国已有五千年栽培历史。皖北多平原地带,黄河故道土地肥沃,适宜种植大豆。2018年春,为响应中国大豆参与世界贸易的竞争,某市农科院积极研究,加大优良品种的培育工作。其中一项基础工作就是研究昼夜温差大小与大豆发芽率之间的关系。为此科研人员分别记录了5天中每天100粒大豆的发芽数得如下数据表格:
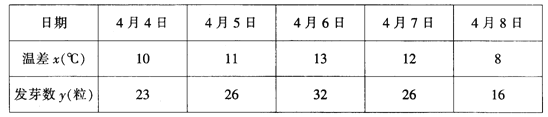
科研人员确定研究方案是:从5组数据中选3组数据求线性回归方程,再用求得的回归方程对剩下的2组数据进行检验.
(1)求剩下的2组数据恰是不相邻的2天数据的概率;
(2)若选取的是4月5日、6日、7日三天数据据此求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与实际数据的误差绝对值均不超过1粒,则认为得到的线性回归方程是可靠的,请检验(Ⅱ)中回归方程是否可靠?
注: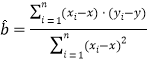
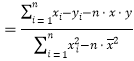 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com