(1)从袋中不放回地取球，求恰好取4次停止的概率P1；

(2)从袋中有放回地取球．

①求恰好取5次停止的概率P2；

②记5次之内(含5次)取到红球的个数为，求随机变量的分布列及数学期望．

【题目】近年来，中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁，百般刁难，并不断加大对各国的施压，拉拢他们抵制华为5G，然而这并没有让华为却步.华为在2018年不仅净利润创下记录，海外增长同样强劲.今年，我国华为某一企业为了进一步增加市场竞争力，计划在2020年利用新技术生产某款新手机.通过市场分析，生产此款手机全年需投入固定成本250万，每生产（千部）手机，需另投入成本万元，且 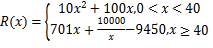，由市场调研知，每部手机售价0.7万元，且全年内生产的手机当年能全部销售完.

（）求出2020年的利润（万元）关于年产量（千部）的函数关系式，（利润=销售额—成本）；

2020年产量为多少（千部）时，企业所获利润最大？最大利润是多少？

【题目】设函数是定义在上的增函数，实数使得对于任意都成立，则实数的取值范围是（ ）

A.B.C.D.

【题目】已知常数，向量， ，经过点，以为方向向量的直线与经过点，以为方向向量的直线交于点，其中．

（）求点的轨迹方程，并指出轨迹．

（）若点，当时， 为轨迹上任意一点，求的最小值．

【题目】已知函数

（1）判断函数的奇偶性，并加以证明；

（2）用定义证明在上是减函数；

（3）函数在上是单调增函数还是单调减函数？（直接写出答案，不要求写证明过程）．

【题目】若对任意， 有唯一确定的与之对应，则称为关于， 的二元函数，现定义满足下列性质的为关于实数， 的广义“距离”．

（）非负性： ，当且仅当时取等号；

（）对称性： ；

（）三角形不等式： 对任意的实数均成立．

给出三个二元函数：①；②；③，

则所有能够成为关于， 的广义“距离”的序号为__________．

A.f（x）=，g（x）=x2–1B.f（x）=，g（x）=x+1

C.f（x）=，g（x）=（）2D.f（x）=|x|，g（t）=

【题目】已知二次函数.

(1)若是的两个不同零点,是否存在实数,使成立?若存在,求的值;若不存在,请说明理由.

(2)设,函数,存在个零点.

(i)求的取值范围;

(ii)设分别是这个零点中的最小值与最大值,求的最大值.

【题目】如图，在三棱柱中，侧棱垂直于底面， ， ， ， ， 分别为， 的中点.

（1）求证：平面平面；

（2）求证：在棱上存在一点，使得平面平面；

（3）求三棱锥的体积．

【题目】某市有一面积为12000平方米的三角形地块，其中边长为200米，现计划建一个如图所示的长方形停车场，停车场的四个顶点都在的三条边上，其余的地面全部绿化.若建停车场的费用为180元/平方米，绿化的费用为60元/平方米，设米，建设工程的总费用为元.

（1）求关于的函数表达式：

（2）求停车场面积最大时的值，并求此时的工程总费用.