A.若事件与事件是互斥事件，则

B.若事件与事件满足条件：，则事件A与事件是对立事件

C.一个人打靶时连续射击两次，则事件“至少有一次中靶”与事件“至多有一次中靶”是对立事件

D.把红、橙、黄3张纸牌随机分给甲、乙、丙3人，每人分得1张，则事件“甲分得红牌”与事件“乙分得红牌”是互斥事件

①两个有共同始点且相等的向量，其终点可能不同；

②若非零向量与共线，则、、、四点共线；

③若非零向量与共线，则；

④四边形是平行四边形，则必有；

⑤，则、方向相同或相反.

A.个B.个C.个D.个

【题目】随着经济的发展，人民的收入水平逐步提高，为了解北京市居民的收入水平，某报社随机调查了名居民的月收入，得到如下的频率分布直方图：

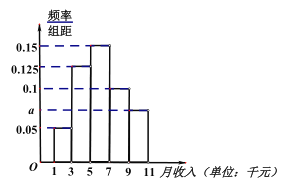
（1）求的值及这名居民的平均月收入（同一组中的数据用该组区间的中点值作代表）

（2）①通过大数据分析，北京人的月收入服从正态分布，其中，，求北京人收入落在的概率；

②将频率视为概率，若北京某公司一部门有人，记这人中月收入落在的人数为，求的数学期望.

附：若，则

（1）若PM⊥PN，求点P坐标；

（2）若圆O上存在点A，B，使得∠APB＝60°，求点P的横坐标的取值范围；

（3）设线段MN的中点为Q，l与x轴的交点为T，求线段TQ长的最大值．

【题目】如图，B,C分别是海岸线上的两个城市，两城市间由笔直的海滨公路相连，B，C之间的距离为100km，海岛A在城市B的正东方50处．从海岛A到城市C，先乘船按北偏西θ角（，其中锐角的正切值为）航行到海岸公路P处登陆，再换乘汽车到城市C．已知船速为25km/h，车速为75km/h.

（1）试建立由A经P到C所用时间与的函数解析式；

（2）试确定登陆点P的位置，使所用时间最少，并说明理由．

【题目】在平面直角坐标系中，已知的顶点，边上中线所在直线方程为，边上的高所在直线方程为，求：

（1）顶点的坐标；

（2）求外接圆的方程．

【题目】已知函数，．

（1）求曲线在点处的切线方程；

（2）若函数，求的单调区间；并证明：当时，；

（3）证明：当时，函数有最小值，设最小值为，求函数的值域．

（1）求图中实数a，b的值；

（2）求所打分值在[6，10]的客户人数；

（3）总公司规定，若4S店的客户回访平均得分低于7分，则将勒令其停业整顿．试用频率分布直方图的组中值对总体平均数进行估计，判断该4S店是否需要停业整顿．

（1）根据茎叶图判断哪种生产方式的效率更高？并说明理由；

（2）求40名工人完成生产任务所需时间的中位数，并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表：

（3）根据（2）中的列联表，能否有99%的把握认为两种生产方式的效率有差异？

附：，

【题目】如图，在正方体中，已知E，F，G，H分别是A1D1，B1C1，D1D，C1C的中点．

（1）求证：EF∥平面ABHG；

（2）求证：平面ABHG⊥平面CFED．