【题目】对于函数与，若存在实数满足，且，则称为的一个点.

(1)证明：函数与不存在的点；

(2)若函数与存在的点，求的范围；

(3)已知函数，证明：存在正实数，对于区间内任意一个皆是函数的点.

【题目】王久良导演的纪录片《垃圾围城》真实地反映了城市垃圾污染问题，目前中国668个城市中有超过的城市处于垃圾的包围之中，且城市垃圾中的快递行业产生的包装垃圾正在逐年攀升，有关数据显示，某城市从2016年到2019年产生的包装垃圾量如下表：

（1）有下列函数模型：①；②；③.试从以上函数模型中，选择模型________（填模型序号），近似反映该城市近几年包装垃圾生产量y（万吨）与年份x的函数关系，并直接写出所选函数模型解析式；

（2）若不加以控制，任由包装垃圾如此增长下去，从哪年开始，该城市的包装垃圾将超过40万吨？（参考数据：）

【题目】某商家通过市场调研，发现某商品的销售价格y（元/件）和销售量x（件）有关，其关系可用图中的折线段表示（不包含端点A）.

（1）把y表示成x的函数；

（2）若该商品进货价格为12元/件，则商家卖出多少件时可以获得最大利润？最大利润为多少元？

A. 50 mB. 100 m

C. 120 mD. 150 m

A. 50 mB. 100 m

C. 120 mD. 150 m

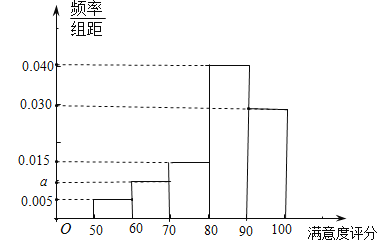
（1）求频率分布直方图中a的值及该样本的中位数

（2）规定：学生对食堂用餐满意度的评分不高于80分为“不满意”，试估计该校在食堂用餐的3000名学生中“不满意”的人数.

(1) 如图，设母球 A 的位置为 (0， 0)，目标球 B 的位置为 (4， 0)，要使目标球 B 向 C(8， -4) 处运动，求母球 A 球心运动的直线方程；

(2)如图，若母球 A 的位置为 (0， -2)，目标球 B 的位置为 (4， 0)，能否让母球 A 击打目标 B 球后，使目标 B 球向 (8，－4) 处运动?

(3)若 A 的位置为 (0，a) 时，使得母球 A 击打目标球 B 时，目标球 B(4， 0) 运动方向可以碰到目标球 C(7，-5)，求 a 的最小值（只需要写出结果即可）

【题目】已知椭圆 C：的离心率为，以短轴为直径的圆被直线 x+y－1 = 0 截得的弦长为．

(1) 求椭圆 C 的方程；

(2) 设 A， B 分别为椭圆的左、右顶点， D 为椭圆右准线 l 与 x 轴的交点， E 为 l上的另一个点，直线 EB 与椭圆交于另一点F，是否存在点 E，使 R)? 若存在，求出点 E 的坐标；若不存在，请说明理由

【题目】已知向量 = (1，2sinθ)，= (sin(θ+)，1)，θR。

(1) 若⊥，求 tanθ的值；

(2) 若∥，且 θ (0，)，求 θ的值

【题目】已知抛物线，点.

（1）求抛物线的顶点坐标；

（2）若抛物线与轴的交点为，连接，并延长交抛物线于点，求证：；

（3）将抛物线作适当的平移，得抛物线，若时，恒成立，求得最大值.