【题目】函数的部分图象如图，M是图象的一个最低点，图象与x轴的一个交点的坐标为，与y轴的交点坐标为.

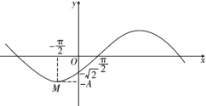
(1)求A，，的值;

(2)若关于x的方程在上有一解，求实数m的取值范围.

【题目】已知：函数，其中．

（Ⅰ）若是的极值点，求的值；

（Ⅱ）求的单调区间；

（Ⅲ）若在上的最大值是，求的取值范围．

规定：人一天行走的步数超过8000步时被系统评定为“积极性”，否则为“懈怠性”.

（1）填写下面列联表（单位：人），并根据列表判断是否有90%的把握认为“评定类型与性别有关”；

附：

（2）为了进一步了解“懈怠性”人群中每个人的生活习惯，从步行数在的人群中再随机抽取3人，求选中的人中男性人数超过女性人数的概率.

（Ⅰ）求证：B1C∥平面A1DE；

（Ⅱ）若AC=3BC=6，△AB1C为等边三角形，求四棱锥A1﹣B1C1ED的体积．

【题目】已知函数f（x）既是二次函数又是幂函数，函数g（x）是R上的奇函数，函数=+1，则h（2018）+h（2017）+h（2016）+…+h（1）+h（0）+h（﹣1）+…h（﹣2016）+h（﹣2017）+h（﹣2018）=___________

【题目】已知.

（1）求的解析式；

（2）求时，的值域：

（3）设，若对任意的，总有恒成立，求实数a的取值范围.

【题目】对于函数，总存在实数，使成立，则称为关于参数的不动点．

（1）当，时，求关于参数的不动点；

（2）若对任意实数，函数恒有关于参数两个不动点，求的取值范围；

（3）当，时，函数在上存在两个关于参数的不动点，试求参数的取值范围．

【题目】为落实国家“精准扶贫”政策，让市民吃上放心蔬菜，某企业于2018年在其扶贫基地投入万元研发资金，用于蔬菜的种植及开发，并计划今后十年内在此基础上，每年投入的资金比上一年增长10%.

（1）写出第年(2019年为第一年)该企业投入的资金数(万元)与的函数关系式，并指出函数的定义域；

（2）该企业从第几年开始(2019年为第一年)，每年投入的资金数将超过万元?

（参考数据）

【题目】现有某高新技术企业年研发费用投入（百万元）与企业年利润（百万元）之间具有线性相关关系，近5年的年科研费用和年利润具体数据如下表：

（1）画出散点图；

（2）求对的回归直线方程；

（3）如果该企业某年研发费用投入8百万元，预测该企业获得年利润为多少？

参考公式：用最小二乘法求回归方程的系数计算公式：

①函数是奇函数，但不是偶函数；

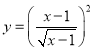②函数与函数表示同一个函数；

③已知函数图象的一条对称轴为，则的值为；

④设函数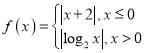，若关于的方程有四个不同的解，且，则的值为.