
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的极大值;
的极大值;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(3)是否存在实数![]() ,使得方程
,使得方程![]() 在
在![]() 上有唯一的根,若存在,求出所有
上有唯一的根,若存在,求出所有![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,E,F分别为边长为2的正方形ABCD的边BC,CD的中点,沿图中虚线折起,使得B,C,D三点重合于点O,点O在平面AEF上的射影H.
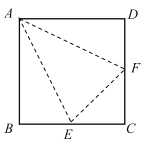
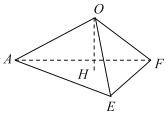
(1)求证:面![]() 面OEA;
面OEA;
(2)求证:点H是![]() 的垂心;
的垂心;
(3)求OH的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,对任意的正整数n,都有
,对任意的正整数n,都有![]() 成立,记
成立,记![]() .
.
(1)求数列![]() 与数列
与数列![]() 的通项公式;
的通项公式;
(2)求证:①![]() 对
对![]() 恒成立.②
恒成立.②![]() 对
对![]() 恒成立,其中
恒成立,其中![]() 为数列
为数列![]() 的前n项和.
的前n项和.
(3)记![]() ,
,![]() 为
为![]() 的前n项和,求证:对任意正整数n,都有
的前n项和,求证:对任意正整数n,都有![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】设A,B分别为双曲线![]() (a>0,b>0)的左、右顶点,双曲线的实轴长为4
(a>0,b>0)的左、右顶点,双曲线的实轴长为4![]() ,焦点到渐近线的距离为
,焦点到渐近线的距离为![]() .
.
(1)求双曲线的方程;
(2)已知直线y=![]() x-2与双曲线的右支交于M,N两点,且在双曲线的右支上存在点D,使
x-2与双曲线的右支交于M,N两点,且在双曲线的右支上存在点D,使![]() ,求t的值及点D的坐标.
,求t的值及点D的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}各项均不相同,a1=1,定义![]() ,其中n,k∈N*.
,其中n,k∈N*.
(1)若![]() ,求
,求![]() ;
;
(2)若bn+1(k)=2bn(k)对![]() 均成立,数列{an}的前n项和为Sn.
均成立,数列{an}的前n项和为Sn.
(i)求数列{an}的通项公式;
(ii)若k,t∈N*,且S1,Sk-S1,St-Sk成等比数列,求k和t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上的动点,点
是圆上的动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]() ,
, ![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,直线
相切,直线![]() 与(1)中所求点
与(1)中所求点![]() 的轨迹交于不同的两点
的轨迹交于不同的两点![]() ,
, ![]() ,
, ![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l1:2x-y+2=0与l2:x+2y-4=0,点P(1, m).
(Ⅰ)若点P到直线l1, l2的距离相等,求实数m的值;
(Ⅱ)当m=1时,已知直线l经过点P且分别与l1, l2相交于A, B两点,若P恰好
平分线段AB,求A, B两点的坐标及直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列五个命题:①过点![]() 的直线方程一定可以表示为
的直线方程一定可以表示为![]() 的形式;②过点
的形式;②过点![]() 且在x,y轴截距相等的直线方程是
且在x,y轴截距相等的直线方程是![]() ;③过点
;③过点![]() 且与直线
且与直线![]() 垂直的直线方程是
垂直的直线方程是![]() ;④设点
;④设点![]() 不在直线
不在直线![]() 上,则过点M且与直线l平行的直线方程是
上,则过点M且与直线l平行的直线方程是![]() ;⑤点
;⑤点![]() 到直线
到直线![]() 的距离不小于2.以上命题中,正确的序号是( )
的距离不小于2.以上命题中,正确的序号是( )
A.②③⑤B.④⑤C.①④⑤D.①③
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某公园内有一个以O为圆心,半径为5百米,圆心角为![]() 的扇形人工湖OAB,OM、ON是分别由OA、OB延伸而成的两条观光道.为便于游客观光,公园的主管部门准备在公园内增建三条观光道,其中一条与
的扇形人工湖OAB,OM、ON是分别由OA、OB延伸而成的两条观光道.为便于游客观光,公园的主管部门准备在公园内增建三条观光道,其中一条与![]() 相切点F,且与OM、ON分别相交于C、D,另两条是分别和湖岸OA、OB垂直的FG、FH (垂足均不与O重合).
相切点F,且与OM、ON分别相交于C、D,另两条是分别和湖岸OA、OB垂直的FG、FH (垂足均不与O重合).
(1) 求新增观光道FG、FH长度之和的最大值;
(2) 在观光道ON段上距离O为15百米的E处的道路两侧各有一个大型娱乐场,为了不影响娱乐场平时的正常开放,要求新增观光道CD的延长线不能进入以E为圆心,2.5百米为半径的圆形E的区域内.则点D应选择在O与E之间的什么位置?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)若函数![]() 的图象在直线
的图象在直线![]() 上方,求
上方,求![]() 的取值范围;
的取值范围;
(3)若函数![]() ,
,![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 的最小值为
的最小值为![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com