
【题目】给出下列五个命题:①过点![]() 的直线方程一定可以表示为
的直线方程一定可以表示为![]() 的形式;②过点
的形式;②过点![]() 且在x,y轴截距相等的直线方程是
且在x,y轴截距相等的直线方程是![]() ;③过点
;③过点![]() 且与直线
且与直线![]() 垂直的直线方程是
垂直的直线方程是![]() ;④设点
;④设点![]() 不在直线
不在直线![]() 上,则过点M且与直线l平行的直线方程是
上,则过点M且与直线l平行的直线方程是![]() ;⑤点
;⑤点![]() 到直线
到直线![]() 的距离不小于2.以上命题中,正确的序号是( )
的距离不小于2.以上命题中,正确的序号是( )
A.②③⑤B.④⑤C.①④⑤D.①③
【答案】B
【解析】
①根据斜率是否存在进行判断;②根据直线可能过原点进行判断;③求得过![]() 且与
且与![]() 垂直的直线方程,由此来进行判断;④求得过
垂直的直线方程,由此来进行判断;④求得过![]() 且平行于
且平行于![]() 的直线方程,由此来进行判断;⑤利用点到直线的距离公式,结合基本不等式来进行判断.
的直线方程,由此来进行判断;⑤利用点到直线的距离公式,结合基本不等式来进行判断.
对于①,过点![]() 的直线方程不一定可以表示为
的直线方程不一定可以表示为![]() 的形式,
的形式,
如斜率不存在时为![]() ,∴①错误;
,∴①错误;
对于②,过点![]() 且在x,y轴截距相等的直线方程是
且在x,y轴截距相等的直线方程是![]() 或
或![]() (过原点),∴②错误;
(过原点),∴②错误;
对于③,过点![]() 且与直线
且与直线![]() 垂直的直线方程可设为
垂直的直线方程可设为
![]() ,
,
代入点M的坐标求得![]() ,
,
故所求的直线方程为![]() ,∴③错误;
,∴③错误;
对于④,设点![]() 不在直线
不在直线![]() 上,
上,
可设过点M且与直线l平行的直线方程为![]() ,代入点M可得
,代入点M可得![]() ,
,
故所求的直线方程是![]() ,④正确;
,④正确;
对于⑤,点![]() 到直线
到直线![]() 的距离为
的距离为
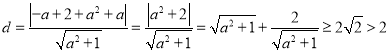 ,
,
当且仅当![]() 时取“=”,∴⑤正确;
时取“=”,∴⑤正确;
综上所述,正确的命题序号是④⑤.
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中x>0,k为常数,e为自然对数的底数.
,其中x>0,k为常数,e为自然对数的底数.
(1)当k≤0时,求![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间(1,3)上存在两个极值点,求实数k的取值范围;
在区间(1,3)上存在两个极值点,求实数k的取值范围;
(3)证明:对任意给定的实数k,存在![]() (
(![]() ),使得
),使得![]() 在区间(
在区间(![]() ,
,![]() )上单调递增.
)上单调递增.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在实数集R上的函数,且y=f(x+1)是偶函数,当x≥1时,f(x)=2x﹣1,则f(![]() ),f(
),f(![]() ),f(
),f(![]() )的大小关系是( )
)的大小关系是( )
A. f(![]() )<f(
)<f(![]() )<f(
)<f(![]() ) B. f(
) B. f(![]() )<f(
)<f(![]() )<f(
)<f(![]() )
)
C. f(![]() )<f(
)<f(![]() )<f(
)<f(![]() ) D. f(
) D. f(![]() )<f(
)<f(![]() )<f(
)<f(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E-ABCD中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() .
.
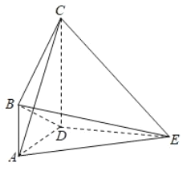
(1)求证:![]() 平面BDE;
平面BDE;
(2)当几何体ABCE的体积等于![]() 时,求四棱锥E-ABCD的侧面积.
时,求四棱锥E-ABCD的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,对任意的正整数n,都有
,对任意的正整数n,都有![]() 成立,记
成立,记![]() .
.
(1)求数列![]() 与数列
与数列![]() 的通项公式;
的通项公式;
(2)求证:①![]() 对
对![]() 恒成立.②
恒成立.②![]() 对
对![]() 恒成立,其中
恒成立,其中![]() 为数列
为数列![]() 的前n项和.
的前n项和.
(3)记![]() ,
,![]() 为
为![]() 的前n项和,求证:对任意正整数n,都有
的前n项和,求证:对任意正整数n,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的两个焦点分别为F1,F2,离心率为
(a>b>0)的两个焦点分别为F1,F2,离心率为![]() ,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
(1)求椭圆C的方程;
(2)若直线y=kx+b与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:①方程![]() 表示的图形是一个点;②命题“若
表示的图形是一个点;②命题“若![]() ,则
,则![]() 或
或![]() ”为真命题;③已知双曲线
”为真命题;③已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,过右焦点
,过右焦点![]() 被双曲线截得的弦长为4的直线有3条;④已知椭圆
被双曲线截得的弦长为4的直线有3条;④已知椭圆![]() 上有两点
上有两点![]() ,
,![]() ,若点
,若点![]() 是椭圆
是椭圆![]() 上任意一点,且
上任意一点,且![]() ,直线
,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() .
.
其中说法正确的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com