
【题目】设集合![]() ,
,![]() 是正数,且
是正数,且![]() .试求交集
.试求交集![]() 的元素个数的最大可能值.
的元素个数的最大可能值.
【答案】见解析
【解析】
不妨设![]() ,且
,且![]() 和
和![]() 都是正整数(
都是正整数(![]() ),但等比数列
),但等比数列![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的各项不一定都是整数,则有
的各项不一定都是整数,则有
![]() .
.
显然,![]() (
(![]() 表示集合
表示集合![]() 的元素个数).下面对公比
的元素个数).下面对公比![]() 分别为有理数和无理数进行讨论.
分别为有理数和无理数进行讨论.
(1)设![]() (
(![]() 与
与![]() 互素,且
互素,且![]() )下面再对
)下面再对![]() 分三种情况进行讨论.
分三种情况进行讨论.
当![]() 时,由
时,由![]() 知
知![]() .由
.由![]() 得
得![]() ,
,![]() ,从而,
,从而,![]() .
.
当![]() 时,由
时,由![]() 知
知![]() .由
.由![]() 得
得![]() ,
,![]() ,从而
,从而![]() .
.
另一方面,确实存在公比为![]() 的6项等比数列:
的6项等比数列:
128,192,288,432,648,972.(如何构造的?)
当![]() 时,
时,![]() ,
,![]() .因为
.因为![]() 与
与![]() 互素,所以
互素,所以![]() ,从而
,从而![]() .由此即得
.由此即得![]() ,
,![]() ,
,![]() .
.
故当![]() 为有理数时,
为有理数时,![]() 的最大可能值是6.
的最大可能值是6.
(2)设![]() 为无理数.由
为无理数.由![]() 为有理数知
为有理数知![]() 为有理数,所以存在最小的正整数
为有理数,所以存在最小的正整数![]() ,使
,使![]() 为有理数(显然
为有理数(显然![]() ).设
).设![]() 被
被![]() 除所得余数为
除所得余数为![]() ,即
,即![]() (
(![]() 和
和![]() 为非负整数,且
为非负整数,且![]() ).由
).由![]() 知
知![]() 为有理数,再由
为有理数,再由![]() 的最小性知只能有
的最小性知只能有![]() ,即
,即![]() .
.
记![]() ,则由上可知
,则由上可知![]() 在
在![]() 中,只须用
中,只须用![]() 来代替
来代替![]() (因为
(因为![]() 中其他的项为无理数),
中其他的项为无理数),![]() 是公比为有理数
是公比为有理数![]() ,首项为
,首项为![]() ,末项为
,末项为![]() 的等比数列,这就化归为公比为有理数的情况(1)了.
的等比数列,这就化归为公比为有理数的情况(1)了.
综合上述即知:![]() 的最大可能值是6.
的最大可能值是6.
注:本题是根据加拿大第四届(1972年)奥林匹克试题第10题改编的.原题为:在公比大于1的等比数列中,最多有几项是在100和1000之间的整数?这是一个佳题.在[1]和别的资料的解答中,都事先假定了等比数列的各项都为整数,其实这样是不严密的(尽管答案是对的),这里给出的解答试图纠正这一不妥之处.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】给出下列五个命题:①过点![]() 的直线方程一定可以表示为
的直线方程一定可以表示为![]() 的形式;②过点
的形式;②过点![]() 且在x,y轴截距相等的直线方程是
且在x,y轴截距相等的直线方程是![]() ;③过点
;③过点![]() 且与直线
且与直线![]() 垂直的直线方程是
垂直的直线方程是![]() ;④设点
;④设点![]() 不在直线
不在直线![]() 上,则过点M且与直线l平行的直线方程是
上,则过点M且与直线l平行的直线方程是![]() ;⑤点
;⑤点![]() 到直线
到直线![]() 的距离不小于2.以上命题中,正确的序号是( )
的距离不小于2.以上命题中,正确的序号是( )
A.②③⑤B.④⑤C.①④⑤D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”![]() 江南梅雨的点点滴滴都流润着浓洌的诗情
江南梅雨的点点滴滴都流润着浓洌的诗情![]() 每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南Q镇
每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南Q镇![]() 年梅雨季节的降雨量
年梅雨季节的降雨量![]() 单位:
单位:![]() 的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
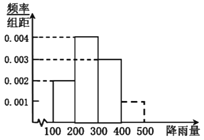
![]() Ⅰ
Ⅰ![]() “梅实初黄暮雨深”
“梅实初黄暮雨深”![]() 假设每年的梅雨天气相互独立,求Q镇未来三年里至少有两年梅雨季节的降雨量超过350mm的概率;
假设每年的梅雨天气相互独立,求Q镇未来三年里至少有两年梅雨季节的降雨量超过350mm的概率;
![]() Ⅱ
Ⅱ![]() “江南梅雨无限愁”
“江南梅雨无限愁”![]() 在Q镇承包了20亩土地种植杨梅的老李也在犯愁,他过去种植的甲品种杨梅,平均每年的总利润为28万元
在Q镇承包了20亩土地种植杨梅的老李也在犯愁,他过去种植的甲品种杨梅,平均每年的总利润为28万元![]() 而乙品种杨梅的亩产量
而乙品种杨梅的亩产量![]() 亩
亩![]() 与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为
与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为![]() 元
元![]() ,请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅可以使总利润
,请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅可以使总利润![]() 万元
万元![]() 的期望更大?
的期望更大?![]() 需说明理由
需说明理由![]()
降雨量 |
|
|
|
|
亩产量 | 500 | 700 | 600 | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 在定义域内存在区间
在定义域内存在区间![]() ,使得该函数在区间
,使得该函数在区间![]() 上的值域为
上的值域为![]() ,则称函数
,则称函数![]() 是该定义域上的“和谐函数”.
是该定义域上的“和谐函数”.
(1)判断函数![]() 是不是“和谐函数”,并说明理由;
是不是“和谐函数”,并说明理由;
(2)若函数![]() 是“和谐函数”,求实数
是“和谐函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图所示,△ABC为正三角形,CE⊥平面ABC,BD∥CE,且CE=AC=2BD,M是AE的中点.

(1)求证:DE=DA;
(2)求证:平面BDM⊥平面ECA;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三顶点坐标分别为
的三顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的外接圆圆M的方程;
的外接圆圆M的方程;
(2)已知动点P在直线![]() 上,过点P作圆M的两条切线PE,PF,切点分别为E,F.
上,过点P作圆M的两条切线PE,PF,切点分别为E,F.
①记四边形PEMF的面积分别为S,求S的最小值;
②证明直线EF恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC的外接圆⊙O的半径为5,CE垂直于⊙O所在的平面,BD∥CE,CE=4,BC=6,且BD=1,![]() .
.
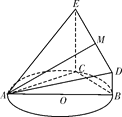
(1)求证:平面AEC⊥平面BCED;
(2)试问线段DE上是否存在点M,使得直线AM与平面ACE所成角的正弦值为![]() ?若存在,确定点M的位置;若不存在,请说明理由.
?若存在,确定点M的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a为实常数).
(a为实常数).
(1)若![]() ,作函数
,作函数![]() 的图象并写出单调减区间;
的图象并写出单调减区间;
(2)当![]() 时,设
时,设![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)当![]() 时对于函数
时对于函数![]() 和函数
和函数![]() ,若对任意的
,若对任意的![]() ,总存在
,总存在![]() 使
使![]() 成立,求实数m的值.
成立,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com