
【题目】已知数列{an}各项均不相同,a1=1,定义![]() ,其中n,k∈N*.
,其中n,k∈N*.
(1)若![]() ,求
,求![]() ;
;
(2)若bn+1(k)=2bn(k)对![]() 均成立,数列{an}的前n项和为Sn.
均成立,数列{an}的前n项和为Sn.
(i)求数列{an}的通项公式;
(ii)若k,t∈N*,且S1,Sk-S1,St-Sk成等比数列,求k和t的值.
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ;(ii)k=2,t=3.
;(ii)k=2,t=3.
【解析】
(1)当![]() 时,由新定义可得
时,由新定义可得![]() ,利用累加法可得结果;
,利用累加法可得结果;
(2)(i)若bn+1(k)=2bn(k)对![]() 均成立,由新定义可得
均成立,由新定义可得![]() ,从而得到数列{an}的通项公式;(ii)由(i)可知Sn=2n-1.因为S1,Sk-S1,St-Sk成等比数列,
,从而得到数列{an}的通项公式;(ii)由(i)可知Sn=2n-1.因为S1,Sk-S1,St-Sk成等比数列,
可得2t-2=(2k-1)2-32k-2+1对k分类讨论可知k和t的值.
(1)因为![]() ,
,
所以![]() ,
,
所以![]() .
.
(2)(i)因为bn+1(k)=2bn(k),
得 ![]() ,
,
令k=1, ![]() ,……………①
,……………①
k=2,![]() ,……………②
,……………②
由①得![]() ,……………③
,……………③
②+③得![]() ,……………④
,……………④
①+④得![]() ,
,
又![]() ,所以数列
,所以数列![]() 是以1为首项,2为公比的等比数列,
是以1为首项,2为公比的等比数列,
所以![]() .
.
(ii)由(i)可知Sn=2n-1.
因为S1,Sk-S1,St-Sk成等比数列,
所以(Sk-S1)2=S1(St-Sk),即(2k-2)2=2t-2k,
所以2t=(2k)2-32k+4,即2t-2=(2k-1)2-32k-2+1(*).
由于Sk-S1≠0,所以k≠1,即k≥2.
当k=2时,2t=8,得t=3.
当k≥3时,由(*),得(2k-1)2-32k-2+1为奇数,
所以t-2=0,即t=2,代入(*)得22k-2-32k-2=0,即2k=3,此时k无正整数解.
综上,k=2,t=3.


科目:高中数学 来源: 题型:
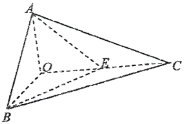
【题目】如图,已知三棱锥O—ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
(1)求异面直线BE与AC所成角的余弦值;
(2)求二面角A—BE—C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(8)的值;
(2)求不等式f(x)-f(x-2)>3的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
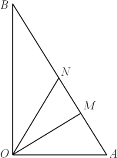
【题目】如图,某镇有一块空地![]() ,其中
,其中![]() ,
,![]() ,
,![]() .当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖
.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖![]() ,其中M,N都在边
,其中M,N都在边![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地带上形成假山,剩下的
地带上形成假山,剩下的![]() 地带开设儿童游乐场.为安全起见,需在
地带开设儿童游乐场.为安全起见,需在![]() 的周围安装防护网.
的周围安装防护网.
(1)当![]() 时,求防护网的总长度;
时,求防护网的总长度;
(2)为节省资金投入,人工湖![]() 的面积要尽可能小,设
的面积要尽可能小,设![]() ,问:当
,问:当![]() 多大时
多大时![]() 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)若函数![]() 的图象在直线
的图象在直线![]() 上方,求
上方,求![]() 的取值范围;
的取值范围;
(3)若函数![]() ,
,![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 的最小值为
的最小值为![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com