
【题目】求平面直角坐标系中格点凸五边形(即每个顶点的纵、横坐标都是整数的凸五边形)的周长的最小值。
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}各项均不相同,a1=1,定义![]() ,其中n,k∈N*.
,其中n,k∈N*.
(1)若![]() ,求
,求![]() ;
;
(2)若bn+1(k)=2bn(k)对![]() 均成立,数列{an}的前n项和为Sn.
均成立,数列{an}的前n项和为Sn.
(i)求数列{an}的通项公式;
(ii)若k,t∈N*,且S1,Sk-S1,St-Sk成等比数列,求k和t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=![]() AB,PH为△PAD边上的高.
AB,PH为△PAD边上的高.
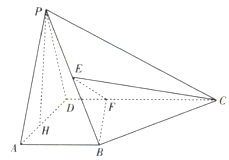
(1)证明:PH⊥平面ABCD;
(2)若PH=1,AD=![]() ,FC=1,求三棱锥E-BCF的体积;
,FC=1,求三棱锥E-BCF的体积;
(3)证明:EF⊥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
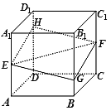
【题目】如图,正方体![]() 的棱长为a,
的棱长为a,![]() 分别是棱
分别是棱![]() 、
、![]() 的中点,过点
的中点,过点![]() 的平面分别与棱
的平面分别与棱![]() 、
、![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:
(1)平面![]() 与平面
与平面![]() 所成角的最大值为
所成角的最大值为![]() ;
;
(2)四边形![]() 的面积的最小值为
的面积的最小值为![]() ;
;
(3)四棱锥![]() 的体积为
的体积为![]() ;
;
(4)点![]() 到平面
到平面![]() 的距离的最大值为
的距离的最大值为![]() ,
,
其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼奧斯(约公元前262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,他证明过这样一个命题:平面内与两定点距离的比为常数k(k>0,k≠1)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.在平面直角坐标系中,设A(﹣3,0),B(3,0),动点M满足![]() =2,则动点M的轨迹方程为()
=2,则动点M的轨迹方程为()
A. (x﹣5)2+y2=16B. x2+(y﹣5)2=9
C. (x+5)2+y2=16D. x2+(y+5)2=9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com