
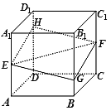
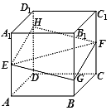
【题目】如图,正方体![]() 的棱长为a,
的棱长为a,![]() 分别是棱
分别是棱![]() 、
、![]() 的中点,过点
的中点,过点![]() 的平面分别与棱
的平面分别与棱![]() 、
、![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:
(1)平面![]() 与平面
与平面![]() 所成角的最大值为
所成角的最大值为![]() ;
;
(2)四边形![]() 的面积的最小值为
的面积的最小值为![]() ;
;
(3)四棱锥![]() 的体积为
的体积为![]() ;
;
(4)点![]() 到平面
到平面![]() 的距离的最大值为
的距离的最大值为![]() ,
,
其中正确的个数为( )
A.1B.2C.3D.4
【答案】C
【解析】
由两平面所成角的余弦公式即面积射影公式,计算可得所求最大值,可判断(1);
由四边形![]() 为菱形,计算面积,考虑
为菱形,计算面积,考虑![]() 的最小值,可判断(2);
的最小值,可判断(2);
由棱锥的等体积法,计算可判断(3);
由等体积法和函数的性质可判断(4);
对于(1),由面面平行的性质定理可得![]() ,可得四边形
,可得四边形![]() 为平行四边形,又直角梯形
为平行四边形,又直角梯形![]() 和直角梯形
和直角梯形![]() 全等,可得
全等,可得![]() ,即有四边形
,即有四边形![]() 为菱形,且
为菱形,且![]() ,由平面
,由平面![]() 在底面上的射影为四边形
在底面上的射影为四边形![]() ,
,
由面积射影公式可得
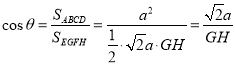
由![]() ,可得
,可得![]() ,可得平面
,可得平面![]() 与平面
与平面![]() 所成角的最大值不为
所成角的最大值不为![]() ,故(1)错;
,故(1)错;
对于(2),由![]() ,可得菱形
,可得菱形![]() 的面积的最小值为
的面积的最小值为![]()
故(2)正确;
对于(3),因为四棱锥![]() 的体积为
的体积为
![]() ,故(3)正确;
,故(3)正确;
对于(4)![]()
![]()
设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,可得
,可得
![]() ,
,
可得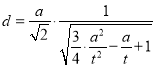 ,(其中
,(其中![]() ),当
),当![]() 即
即![]() 时,
时,
![]() 取得最大值
取得最大值![]() ,故(4)正确;
,故(4)正确;
故选:C


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 命题![]() :
:![]() ,
,![]() ,则命题
,则命题![]() :
:![]() ,
,![]()
B. “![]() ”是“
”是“![]() ”的充要条件
”的充要条件
C. 命题“若![]() ,则
,则![]() 或
或![]() ”的逆否命题是“若
”的逆否命题是“若![]() 或
或![]() ,则
,则![]() ”
”
D. 命题![]() :
:![]() ,
,![]() ;命题
;命题![]() :对
:对![]() ,总有
,总有![]() ;则
;则![]() 是真命题
是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间![]() 上的函数
上的函数![]() 的图象关于直线
的图象关于直线![]() 对称,当
对称,当![]() 时,函数
时,函数![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的表达式;
的表达式;
(3)若关于![]() 的方程
的方程![]() 有解,那么将方程在
有解,那么将方程在![]() 取某一确定值时所求得的所有解的和记为
取某一确定值时所求得的所有解的和记为![]() ,求
,求![]() 的所有可能值及相应
的所有可能值及相应![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,港口![]() 在港口
在港口![]() 的正东120海里处,小岛
的正东120海里处,小岛![]() 在港口
在港口![]() 的北偏东
的北偏东![]() 的方向,且在港口
的方向,且在港口![]() 北偏西
北偏西![]() 的方向上,一艘科学考察船从港口
的方向上,一艘科学考察船从港口![]() 出发,沿北偏东
出发,沿北偏东![]() 的
的![]() 方向以20海里/小时的速度驶离港口
方向以20海里/小时的速度驶离港口![]() .一艘给养快艇从港口
.一艘给养快艇从港口![]() 以60海里/小时的速度驶向小岛
以60海里/小时的速度驶向小岛![]() ,在
,在![]() 岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
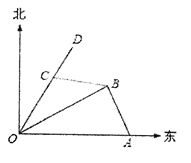
(1)求给养快艇从港口![]() 到小岛
到小岛![]() 的航行时间;
的航行时间;
(2)给养快艇驶离港口![]() 后,最少经过多少小时能和科考船相遇?
后,最少经过多少小时能和科考船相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com