
【题目】已知定义在区间![]() 上的函数
上的函数![]() 的图象关于直线
的图象关于直线![]() 对称,当
对称,当![]() 时,函数
时,函数![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的表达式;
的表达式;
(3)若关于![]() 的方程
的方程![]() 有解,那么将方程在
有解,那么将方程在![]() 取某一确定值时所求得的所有解的和记为
取某一确定值时所求得的所有解的和记为![]() ,求
,求![]() 的所有可能值及相应
的所有可能值及相应![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)过点![]() (e是自然对数的底数)作函数
(e是自然对数的底数)作函数![]() 图象的切线l,求直线l的方程;
图象的切线l,求直线l的方程;
(2)求函数![]() 在区间
在区间![]() (
(![]() )上的最大值;
)上的最大值;
(3)若![]() ,且
,且![]() 对任意
对任意![]() 恒成立,求k的最大值.(参考数据:
恒成立,求k的最大值.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=![]() AB,PH为△PAD边上的高.
AB,PH为△PAD边上的高.
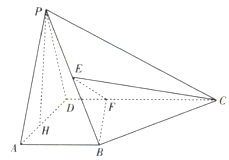
(1)证明:PH⊥平面ABCD;
(2)若PH=1,AD=![]() ,FC=1,求三棱锥E-BCF的体积;
,FC=1,求三棱锥E-BCF的体积;
(3)证明:EF⊥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为a,
的棱长为a,![]() 分别是棱
分别是棱![]() 、
、![]() 的中点,过点
的中点,过点![]() 的平面分别与棱
的平面分别与棱![]() 、
、![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:
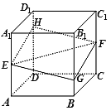
(1)平面![]() 与平面
与平面![]() 所成角的最大值为
所成角的最大值为![]() ;
;
(2)四边形![]() 的面积的最小值为
的面积的最小值为![]() ;
;
(3)四棱锥![]() 的体积为
的体积为![]() ;
;
(4)点![]() 到平面
到平面![]() 的距离的最大值为
的距离的最大值为![]() ,
,
其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台为宣传本省,随机对本省内15~65岁的人群抽取了![]() 人,回答问题“本省内著名旅游景点有哪些”统计结果如图表所示.
人,回答问题“本省内著名旅游景点有哪些”统计结果如图表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 |
|
|
|
第2组 |
| 18 |
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|

(1)分别求出![]() 的值;
的值;
(2)从第2、3、4组回答正确的人中用分层抽样的方法抽取6人,求第2、3、4组每组各抽取多少人?
(3)指出直方图中,这组数据的中位数是多少(取整数值)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:kx-y+4=0与直线l2:x+ky-3=0相交于点P,则当实数k变化时,点P到直线4x-3y+10=0的距离的最大值为( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com