
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() 分别为
分别为![]() 中点,且
中点,且![]() ,
,![]() .
.
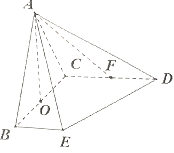
(1)![]() 平面
平面![]() ;
;
(2)若![]() 为线段
为线段![]() 上一点,且
上一点,且![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(3)求二面角![]() 的大小.
的大小.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连结![]() ,利用勾股定理逆定理可证明
,利用勾股定理逆定理可证明![]() ,又易证
,又易证![]() ,可证明
,可证明![]() 平面
平面![]() (2)连接
(2)连接![]() ,根据
,根据![]() ,
,![]() 平面
平面![]() 可得
可得![]() ,进而
,进而![]() ,利用
,利用![]() 为
为![]() 中点可得结论(3)取
中点可得结论(3)取![]() 的中点
的中点![]() 连结
连结![]() ,由(1)知
,由(1)知![]() ,且
,且![]() ,
,![]() ,建立空间直角坐标系
,建立空间直角坐标系![]() ,求平面
,求平面![]() ,平面
,平面![]() 的法向量,计算其夹角即可.
的法向量,计算其夹角即可.
(1)证明:连结![]()
![]() ,
,![]() 为
为![]() 的中点
的中点
![]() ,且
,且![]() ,
,![]()
又![]() ,
,![]() 是
是![]() 中点,
中点,![]() ,
,
![]()
由已知![]() ,
,![]()
![]() ,且
,且![]() 是平面
是平面![]() 内两条相交直线
内两条相交直线
![]() 平面
平面![]() .
.
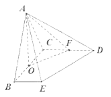
(2)连接![]() ,由已知底面
,由已知底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]()
则四边形![]() 为平行四边形
为平行四边形
所以![]()
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]()
所以![]()
因为![]() 为
为![]() 中点,所以
中点,所以![]() 为
为![]() 中点
中点
所以![]() ,又因为点
,又因为点![]() 为
为![]() 的中点.
的中点.
所以![]() .
.
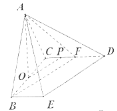
(3)取![]() 的中点
的中点![]() 连结
连结![]() ,由(1)知
,由(1)知![]() ,且
,且![]() ,
,![]() ,
,
如图,建立空间直角坐标系![]() .
.
因为![]()
所以![]() ,
,![]() ,
,![]()
![]() ,
,![]()
由于![]() 平面
平面![]() ,所以平面
,所以平面![]() 的法向量
的法向量![]()
设平面![]() 的法向量
的法向量![]() ,则有
,则有
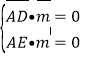 即
即![]()
令![]() ,则
,则![]() ,
,![]() ,即
,即![]()
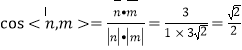
由题知二面角![]() 为锐二面角
为锐二面角
所以二面角![]() 的大小为
的大小为![]() .
.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】已知定义在区间![]() 上的函数
上的函数![]() 的图象关于直线
的图象关于直线![]() 对称,当
对称,当![]() 时,函数
时,函数![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的表达式;
的表达式;
(3)若关于![]() 的方程
的方程![]() 有解,那么将方程在
有解,那么将方程在![]() 取某一确定值时所求得的所有解的和记为
取某一确定值时所求得的所有解的和记为![]() ,求
,求![]() 的所有可能值及相应
的所有可能值及相应![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,点
,点![]() 为
为![]() 上异于顶点的任意一点,过
上异于顶点的任意一点,过![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,且有
,且有![]() ,当点
,当点![]() 的横坐标为3时,
的横坐标为3时,![]() 为正三角形.
为正三角形.
(1)求![]() 的方程;
的方程;
(2)若直线![]() ,且
,且![]() 和
和![]() 相切于点
相切于点![]() ,试问直线
,试问直线![]() 是否过定点,若过定点,求出定点坐标;若不过定点,说明理由.
是否过定点,若过定点,求出定点坐标;若不过定点,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
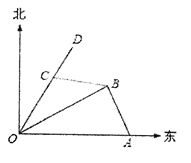
【题目】如图,港口![]() 在港口
在港口![]() 的正东120海里处,小岛
的正东120海里处,小岛![]() 在港口
在港口![]() 的北偏东
的北偏东![]() 的方向,且在港口
的方向,且在港口![]() 北偏西
北偏西![]() 的方向上,一艘科学考察船从港口
的方向上,一艘科学考察船从港口![]() 出发,沿北偏东
出发,沿北偏东![]() 的
的![]() 方向以20海里/小时的速度驶离港口
方向以20海里/小时的速度驶离港口![]() .一艘给养快艇从港口
.一艘给养快艇从港口![]() 以60海里/小时的速度驶向小岛
以60海里/小时的速度驶向小岛![]() ,在
,在![]() 岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
(1)求给养快艇从港口![]() 到小岛
到小岛![]() 的航行时间;
的航行时间;
(2)给养快艇驶离港口![]() 后,最少经过多少小时能和科考船相遇?
后,最少经过多少小时能和科考船相遇?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() (
(![]() ),且
),且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 有区间
有区间![]() 上有一个零点,求实数
上有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com