
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,点
,点![]() 为
为![]() 上异于顶点的任意一点,过
上异于顶点的任意一点,过![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,且有
,且有![]() ,当点
,当点![]() 的横坐标为3时,
的横坐标为3时,![]() 为正三角形.
为正三角形.
(1)求![]() 的方程;
的方程;
(2)若直线![]() ,且
,且![]() 和
和![]() 相切于点
相切于点![]() ,试问直线
,试问直线![]() 是否过定点,若过定点,求出定点坐标;若不过定点,说明理由.
是否过定点,若过定点,求出定点坐标;若不过定点,说明理由.
【答案】(1) ![]() (2) 直线
(2) 直线![]() 过定点
过定点![]() .
.
【解析】
(1)设![]() ,抛物线的焦点为
,抛物线的焦点为![]() ,由
,由![]() ,可得
,可得![]() ,从而
,从而![]() ,再由
,再由![]() 点横坐标与
点横坐标与![]() 中点横坐标相同可求得
中点横坐标相同可求得![]() .
.
(2)设![]() ,可得
,可得![]() ,由
,由![]() ,可设直线
,可设直线![]() 的方程为
的方程为![]() ,由它与抛物线相切可求得
,由它与抛物线相切可求得![]() ,也即得出
,也即得出![]() 点坐标,求出直线
点坐标,求出直线![]() 方程,观察得其过定点.注意分类,即按直线
方程,观察得其过定点.注意分类,即按直线![]() 斜率是否存在分类讨论.
斜率是否存在分类讨论.
(1)抛物线的焦点![]() ,设
,设![]() ,则
,则![]() 的中点坐标为
的中点坐标为![]() ,
,
∵![]() ,∴
,∴![]() ,解得
,解得![]() ,或
,或![]() (舍),
(舍),
∵![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
∴抛物线方程为![]() .
.
(2)由(1)知,![]() ,设
,设![]() ,
,![]() ,
,
∵![]() ,则
,则![]() ,由
,由![]() 得
得![]() ,即
,即![]() ,
,
∴直线![]() 的斜率
的斜率![]() ,∵
,∵![]() ,故设直线
,故设直线![]() 的方程为
的方程为![]() ,
,
联立方程组 ,得
,得![]() ,
,
∵直线![]() 与抛物线相切,∴
与抛物线相切,∴![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
∵![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() ,∴直线
,∴直线![]() 过定点
过定点![]() ,
,
当![]() 时,直线
时,直线![]() 方程为
方程为![]() ,经过定点
,经过定点![]() ,
,
综上,直线![]() 过定点
过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】甲、乙两地相距![]() ,汽车从甲地匀速行驶到乙地,速度不超过
,汽车从甲地匀速行驶到乙地,速度不超过![]() .已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
.已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度![]() (单位:
(单位:![]() )的平方成正比,且比例系数为
)的平方成正比,且比例系数为![]() ,固定部分为
,固定部分为![]() 元.
元.
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() 的函数,并求出当
的函数,并求出当![]() ,
,![]() 时,汽车应以多大速度行驶,才能使得全程运输成本最小;
时,汽车应以多大速度行驶,才能使得全程运输成本最小;
(2)随着汽车的折旧,运输成本会发生一些变化,那么当![]() ,
,![]() 元,此时汽车的速度应调整为多大,才会使得运输成本最小.
元,此时汽车的速度应调整为多大,才会使得运输成本最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,港口![]() 在港口
在港口![]() 的正东120海里处,小岛
的正东120海里处,小岛![]() 在港口
在港口![]() 的北偏东
的北偏东![]() 的方向,且在港口
的方向,且在港口![]() 北偏西
北偏西![]() 的方向上,一艘科学考察船从港口
的方向上,一艘科学考察船从港口![]() 出发,沿北偏东
出发,沿北偏东![]() 的
的![]() 方向以20海里/小时的速度驶离港口
方向以20海里/小时的速度驶离港口![]() .一艘给养快艇从港口
.一艘给养快艇从港口![]() 以60海里/小时的速度驶向小岛
以60海里/小时的速度驶向小岛![]() ,在
,在![]() 岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
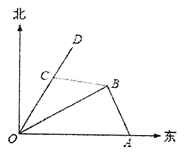
(1)求给养快艇从港口![]() 到小岛
到小岛![]() 的航行时间;
的航行时间;
(2)给养快艇驶离港口![]() 后,最少经过多少小时能和科考船相遇?
后,最少经过多少小时能和科考船相遇?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】恩格尔系数(记为![]() )是指居民的食物支出占家庭消费总支出的比重.国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况.联合国对消费水平的规定标准如下表:
)是指居民的食物支出占家庭消费总支出的比重.国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况.联合国对消费水平的规定标准如下表:
家庭类型 | 贫穷 | 温饱 | 小康 | 富裕 | 最富裕 |
|
|
|
|
|
|
实施精准扶贫以来,根据对某山区贫困家庭消费支出情况(单位:万元)的抽样调查,2018年每个家庭平均消费支出总额为2万元,其中食物消费支出为1.2万元预测2018年到2020年每个家庭平均消费支出总额每年的增长率约是30%,而食物消费支出平均每年增加0.2万元,预测该山区的家庭2020年将处于( )
A.贫困水平B.温饱水平C.小康水平D.富裕水平
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设曲线![]() 在原点处切线与直线
在原点处切线与直线![]() 垂直,则a=______.
垂直,则a=______.
(2)已知等差数列![]() 中,已知
中,已知![]() ,则
,则![]() =________________.
=________________.
(3)若函数![]() ,则
,则![]() __________.
__________.
(4)曲线![]() 与直线
与直线![]() 及
及![]() 轴围成的图形的面积为__________.
轴围成的图形的面积为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com