练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知f（x）是定义在（0，+∞）上的增函数，且满足f（xy）=f（x）+f（y），f（2）=1．

    （1）求f（8）的值；

    （2）求不等式f（x）-f（x-2）＞3的解集．

    【答案】（1）3 （2）

    【解析】

    试题分析：（Ⅰ）利用已知条件，直接通过f（8）=f（4）+f（2），f（4）=f（2）+f（2）求解f（8）；（Ⅱ）利用已知条件转化不等式f（x）+f（x-2）＞3为不等式组，即可求解不等式的解集

    试题解析：（1）由题意可得f（8）=f（4×2）=f（4）+f（2）=f（2×2）+f（2）=3f（2）="3"

    （2）原不等式可化为f（x）＞f（x-2）+3=f（x-2）+f（8）=f（8x-16）

    ∵f（x）是定义在（0，+∞）上的增函数

    ∴

    解得：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校从参加高三模拟考试的学生中随机抽取60名学生，按其数学成绩（均为整数）分成六组， ，…， 后得到如下部分频率分布直方图，观察图中的信息，回答下列问题：

    （1）补全频率分布直方图；

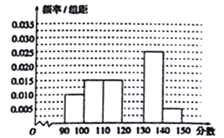
    （2）估计本次考试的数学平均成绩（同一组中的数据用该组区间的中点值作代表）；

    （3）用分层抽样的方法在分数段为的学生成绩中抽取一个容量为6的样本，再从这6个样本中任取2人成绩，求至多有1人成绩在分数段内的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|ax﹣1|
    （1）若f（x）≤2的解集为[﹣3，1]，求实数a的值；
    （2）若a=1，若存在x∈R，使得不等式f（2x+1）﹣f（x﹣1）≤3﹣2m成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知常数数列的前项和为，且

    （1）求数列的通项公式；

    （2）若且数列是单调递增数列，求实数的取值范围；

    （3）若数列满足：对于任意给定的正整数，是否存在使 ?若存在，求的值（只要写出一组即可）；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列满足.

    （1）求的通项公式；

    （2）设等比数列满足，问： 与数列的第几项相等？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面内动点P与点A（﹣3，0）和点B（3，0）的连线的斜率之积为﹣ ．
    （1）求动点P的轨迹方程；
    （2）设点P的轨迹且曲线C，过点（1，0）的直线与曲线C交于M，N两点，记△AMB的面积为S1 ， △ANB的面积为S2 ， 当S1﹣S2取得最大值时，求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=xlnx，g（x）= ．
    （1）证明方程f（x）=g（x）在区间（1，2）内有且仅有唯一实根；
    （2）记max{a，b}表示a，b两个数中的较大者，方程f（x）=g（x）在区间（1，2）内的实数根为x0 ， m（x）=max{f（x），g（x）}，若m（x）=n（n∈R）在（1，+∞）内有两个不等的实根x1 ， x2（x1＜x2），判断x1+x2与2x0的大小，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱柱ABC﹣A1B1C1中，AA1⊥面ABC，AB⊥AC，且AA1=AB=AC，则异面直线AB1与BC1所成角为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,多面体ABCDE中，四边形ABED是直角梯形，∠BAD=90°，DE∥AB，△ACD是的正三角形，CD=AB=DE=1，BC=

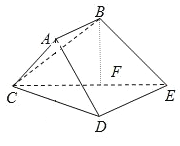
    （1）求证：△CDE是直角三角形

    （2） F是CE的中点，证明：BF⊥平面CDE

    查看答案和解析>>

    同步练习册答案