
【题目】如图,多面体ABCDE中,四边形ABED是直角梯形,∠BAD=90°,DE∥AB,△ACD是的正三角形,CD=AB=![]() DE=1,BC=
DE=1,BC=![]()
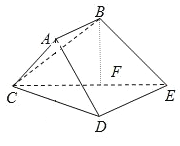
(1)求证:△CDE是直角三角形
(2) F是CE的中点,证明:BF⊥平面CDE
【答案】(1)见解析;(2)见解析
【解析】
(1)根据勾股定理先证明AB⊥AC,结合AB⊥AD,即可证出AB⊥平面ACD,又DE∥AB所以DE⊥平面ACD,即可证明△CDE是直角三角形.
(2) 取CD中点M,连接AM、MF. 先证出MF⊥平面ACD即可得平面CDE⊥平面ACD,利用面面垂直的性质定理可证得AM⊥面CDE,又AM∥BF,即可证出BF⊥平面CDE.
(1)证明:∵∠BAD=90°∴AB⊥AD
△ACD是的正三角形,CD=AB=1,BC=![]() ,
,
∴△ABC是直角三角形,AB⊥AC
∴AB⊥平面ACD
∵DE∥AB
∴DE⊥平面ACD
∴△CDE是直角三角形
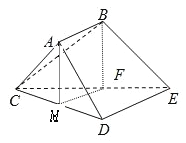
(2)证明:取CD中点M,连接AM、MF.
∵F是CE的中点
∴AMFB是平行四边形
∴MF∥AB,AM∥BF
∴MF⊥平面ACD
∵MF在平面ECD内
∴平面CDE⊥平面ACD
∵△ACD是的正三角形,M是CD中点
∴AM⊥CD
平面CED∩平面ACD=CD,∴AM⊥面CDE,
∵AM∥BF,
∴BF⊥平面CDE


科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(8)的值;
(2)求不等式f(x)-f(x-2)>3的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】. (12分)如图所示,函数![]() 的一段图象过点
的一段图象过点![]() .
.
(1)求函数![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得函数
个单位,得函数![]() 的图象,求函数
的图象,求函数![]() 的最大值,并求此时自变量
的最大值,并求此时自变量![]() 的取值集合.
的取值集合.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有标号为![]() ,
,![]() ,
,![]() 的
的![]() 个小球,其中标号
个小球,其中标号![]() 的小球有
的小球有![]() 个,标号
个,标号![]() 的小球有
的小球有![]() 个,标号
个,标号![]() 的小球有
的小球有![]() 个,现从口袋中随机摸出
个,现从口袋中随机摸出![]() 个小球.
个小球.
(![]() )求摸出
)求摸出![]() 个小球标号之和为偶数的概率.
个小球标号之和为偶数的概率.
(![]() )用
)用![]() 表示摸出
表示摸出![]() 个小球的标号之和,写出
个小球的标号之和,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列几个命题
①奇函数的图象一定通过原点
②函数![]() 是偶函数,但不是奇函数
是偶函数,但不是奇函数
③函数f(x)=ax﹣1+3的图象一定过定点P,则P点的坐标是(1,4)
④若f(x+1)为偶函数,则有f(x+1)=f(﹣x﹣1)
⑤若函数 在R上的增函数,则实数a的取值范围为[4, 8)
在R上的增函数,则实数a的取值范围为[4, 8)
其中正确的命题序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售岀8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com