
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售岀8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
【答案】(1) y=-![]() ; (2) 200元;(3) 每台冰箱的售价降价150元时,商场的利润最高,最高利润是5000元
; (2) 200元;(3) 每台冰箱的售价降价150元时,商场的利润最高,最高利润是5000元
【解析】
(1)先计算降价后每台冰箱的利润,然后计算每天销售额,两者相乘得到利润的表达式.(2)令利润的表达式等于![]() ,解出降价的钱,从中选一个百姓能得到更大优惠的.(3)利用二次函数的对称轴,求得函数的最大值以及相应的自变量的值.
,解出降价的钱,从中选一个百姓能得到更大优惠的.(3)利用二次函数的对称轴,求得函数的最大值以及相应的自变量的值.
(1)根据题意,得y=(2400-2000-x)(8+4×![]() ),
),
即y=-![]() ;
;
(2)由题意,得-![]()
整理,得x2-300x+20000=0,
解这个方程,得x1=100,x2=200,
要使百姓得到实惠,取x=200,
所以,每台冰箱应降价200元;
(3)对于y=-![]()
当x=-![]() 时,y最大值=(2400-2000-150)(8+4×
时,y最大值=(2400-2000-150)(8+4×![]() )=250×20=5000,
)=250×20=5000,
所以,每台冰箱的售价降价150元时,商场的利润最高,最高利润是5000元。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDE中,四边形ABED是直角梯形,∠BAD=90°,DE∥AB,△ACD是的正三角形,CD=AB=![]() DE=1,BC=
DE=1,BC=![]()
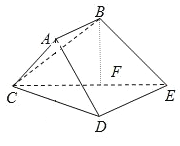
(1)求证:△CDE是直角三角形
(2) F是CE的中点,证明:BF⊥平面CDE
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() .
.

(1)已画出函数![]() 在
在![]() 轴左侧的图像,如图所示,请补出完整函数
轴左侧的图像,如图所示,请补出完整函数![]() 的图像,并根据图像写出函数
的图像,并根据图像写出函数![]() 的增区间;
的增区间;
⑵写出函数![]() 的解析式和值域.
的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 过焦点
过焦点![]() 交抛物线于
交抛物线于![]() 两点,
两点, ![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若点![]() 是抛物线
是抛物线![]() 位于曲线
位于曲线![]() (
(![]() 为坐标原点)上一点,求
为坐标原点)上一点,求![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+bx(其中a,b为常数,a>0且a≠1,b>0且b≠1)的图象经过点A(1,6),![]() .
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若a>b,函数![]() ,求函数g(x)在[-1,2]上的值域.
,求函数g(x)在[-1,2]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=x3cos3(x+ ![]() ),下列说法正确的是( )
),下列说法正确的是( )
A.f(x)是奇函数且在(﹣ ![]() ,
, ![]() )上递增
)上递增
B.f(x)是奇函数且在(﹣ ![]() ,
, ![]() )上递减
)上递减
C.f(x)是偶函数且在(0, ![]() )上递增
)上递增
D.f(x)是偶函数且在(0, ![]() )上递减
)上递减
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com