
【题目】已知函数f(x)=xlnx,g(x)= ![]() .
.
(1)证明方程f(x)=g(x)在区间(1,2)内有且仅有唯一实根;
(2)记max{a,b}表示a,b两个数中的较大者,方程f(x)=g(x)在区间(1,2)内的实数根为x0 , m(x)=max{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)内有两个不等的实根x1 , x2(x1<x2),判断x1+x2与2x0的大小,并说明理由.
【答案】
(1)证明:令F(x)=f(x)﹣g(x),
则F(x)=xlnx﹣ ![]() ,定义域是(0,+∞),
,定义域是(0,+∞),
F′(x)=1+lnx+ ![]() ,
,
x>1时,F′(x)>0,∴F(x)在(1,2)递增,
又F(1)=﹣ ![]() <0,F(2)=2ln2﹣
<0,F(2)=2ln2﹣ ![]() >0,
>0,
而F(x)在(1,+∞)上连续,
根据零点存在定理可得:F(x)=0在区间(1,2)有且只有1个实根,
即方程f(x)=g(x)在区间(1,2)内有且仅有唯一实根
(2)解:x1+x2<2x0,
证明过程如下:
显然:m(x)= 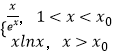 ,
,
当1<x<x0时,m(x)= ![]() ,m′(x)=
,m′(x)= ![]() <0,
<0,
故m(x)单调递减;
当x>x0时,m(x)=xlnx,m′(x)=1+lnx>0,m(x)递增,
要证x1+x2<2x0,
即证x2<2x0﹣x1,
由(1)知x1<x0<x2,g(x1)=f(x2)=n,
故即证f(x2)<f(2x0﹣x1),
即证g(x1)<f(2x0﹣x1),
即证 ![]() <(2x0﹣x1)ln(2x0﹣x1),(1<x1<x0<2),(*),
<(2x0﹣x1)ln(2x0﹣x1),(1<x1<x0<2),(*),
设H(x)= ![]() ﹣(2x0﹣x)ln(2x0﹣x),(1<x<x0<2),
﹣(2x0﹣x)ln(2x0﹣x),(1<x<x0<2),
H′(x)= ![]() +ln(2x0﹣x)+1,
+ln(2x0﹣x)+1,
∵1<x<x0<2,
∴ ![]() +1>0,ln(2x0﹣x)>0,
+1>0,ln(2x0﹣x)>0,
∴H′(x)>0,
∴H(x)在(1,x0)递增,
即H(x)<H(x0)=0,故(*)成立,
故x1+x2<2x0成立
【解析】(1)求出函数的导数,通过解关于导函数的不等式,得到函数的单调性,结合零点存在定理证出结论即可;(2)问题转化为证 ![]() <(2x0﹣x1)ln(2x0﹣x1),(1<x1<x0<2),(*),设H(x)=
<(2x0﹣x1)ln(2x0﹣x1),(1<x1<x0<2),(*),设H(x)= ![]() ﹣(2x0﹣x)ln(2x0﹣x),(1<x<x0<2),根据函数的单调性证明即可.
﹣(2x0﹣x)ln(2x0﹣x),(1<x<x0<2),根据函数的单调性证明即可.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.


科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图.

记![]() 表示
表示![]() 台机器在三年使用期内需更换的易损零件数,
台机器在三年使用期内需更换的易损零件数,![]() 表示
表示![]() 台机器在购买易损零件上所需的费用(单位:元),
台机器在购买易损零件上所需的费用(单位:元),![]() 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)若要求 “需更换的易损零件数不大于![]() ”的频率不小于
”的频率不小于![]() ,求
,求![]() 的最小值;
的最小值;
(3)假设这![]() 台机器在购机的同时每台都购买
台机器在购机的同时每台都购买![]() 个易损零件,或每台都购买
个易损零件,或每台都购买![]() 个易损零件,分别计算这
个易损零件,分别计算这![]() 台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买
台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买![]() 台机器的同时应购买
台机器的同时应购买![]() 个还是
个还是![]() 个易损零件?
个易损零件?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商小王对其所经营的某一型号二手汽车的使用年数![]() (0<
(0<![]() ≤10)与销售价格
≤10)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅰ)试求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(附:回归方程![]() 中,
中,
(Ⅱ)已知每辆该型号汽车的收购价格为![]() 万元,根据(Ⅰ)中所求的回归方程,
万元,根据(Ⅰ)中所求的回归方程,
预测![]() 为何值时,小王销售一辆该型号汽车所获得的利润
为何值时,小王销售一辆该型号汽车所获得的利润![]() 最大.
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(8)的值;
(2)求不等式f(x)-f(x-2)>3的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某台风中心位于海港城市![]() 东偏北
东偏北![]() 的150公里外,以每小时
的150公里外,以每小时![]() 公里的速度向正西方向快速移动,2.5小时后到达距海港城市
公里的速度向正西方向快速移动,2.5小时后到达距海港城市![]() 西偏北
西偏北![]() 的200公里处,若
的200公里处,若![]() ,则风速
,则风速![]() 的值为_____公里/小时
的值为_____公里/小时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,上焦点
,上焦点![]() 到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=
到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=![]() .
.
(I)若P是椭圆C上任意一点,求![]() 的取值范围;
的取值范围;
(II)设过椭圆C的上顶点A的直线![]() 与椭圆交于点B(B不在y轴上),垂直于
与椭圆交于点B(B不在y轴上),垂直于![]() 的直线与
的直线与![]() 交于点M,与
交于点M,与![]() 轴交于点H,若
轴交于点H,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】. (12分)如图所示,函数![]() 的一段图象过点
的一段图象过点![]() .
.
(1)求函数![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得函数
个单位,得函数![]() 的图象,求函数
的图象,求函数![]() 的最大值,并求此时自变量
的最大值,并求此时自变量![]() 的取值集合.
的取值集合.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com