【题目】已知函数图象相邻两条对称轴之间的距离为，将函数的图象向左平移个单位，得到的图象关于轴对称，则（ ）

A. 函数的周期为 B. 函数图象关于点对称

C. 函数图象关于直线对称 D. 函数在上单调

【题目】已知斜三棱柱的棱长都是，侧棱与底面成60°角，侧面底面.

（1）求证：；

（2）求平面与平面所成的锐二面角的大小.

【题目】已知的三顶点坐标分别为，，．

（1）求的外接圆圆M的方程；

（2）已知动点P在直线上，过点P作圆M的两条切线PE,PF，切点分别为E,F.

①记四边形PEMF的面积分别为S，求S的最小值；

②证明直线EF恒过定点.

【题目】如图，AB为半圆O的直径，点C为半圆上一点，，平面ABC，D为PA中点，.

（1）求证：；

（2）求直线BD与平面PBC所成角的正弦值.

（1）求线性回归方程；

（2）估计使用年限为12年时，使用该款车的总费用是多少万元?

线性回归方程中斜率和截距用最小二乘法估计计算公式如下：，

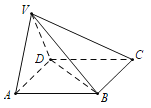
（Ⅰ）证明AB⊥平面VAD；

（Ⅱ）求面VAD与面VDB所成二面角的大小．

【题目】设集合，是正数，且.试求交集的元素个数的最大可能值.

若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.

（1）将频率视为概率，估计我校7000名学生中“锻炼达人”有多少?

（2）从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.

①求男生和女生各抽取了多少人；

②若从这5人中随机抽取2人作为组长候选人，求抽取的2人中男生和女生各1人的概率.

【题目】设集合.若的非空子集中奇数的个数大于偶数的个数，则称是“好的”.试求的所有“好的”子集的个数（答案写成最简结果）.