
科目: 来源: 题型:
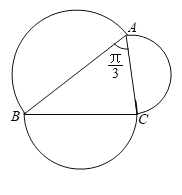
【题目】定义在封闭的平面区域D内任意两点的距离的最大值称为平面区域D的“直径".已知锐角三角形的三个顶点A,B,C在半径为1的圆上,且![]() ,分别以
,分别以![]() 各边为直径向外作三个半圆,这三个半圆和
各边为直径向外作三个半圆,这三个半圆和![]() 构成平面区域D,则平面区域D的“直径”是______.
构成平面区域D,则平面区域D的“直径”是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.![]() 是自然对数的底数.
是自然对数的底数.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .求实数
.求实数![]() 的值;
的值;
(2)① 若![]() 时,函数
时,函数![]() 既有极大值,又有极小值,求实数
既有极大值,又有极小值,求实数![]() 的取值范围;
的取值范围;
② 若![]() ,
,![]() .若
.若![]() 对一切正实数
对一切正实数![]() 恒成立,求实数
恒成立,求实数![]() 的最大值(用
的最大值(用![]() 表示).
表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 、
、![]() 满足
满足![]() ,
,![]() ,其中
,其中![]() ,则称
,则称![]() 为
为![]() 的“生成数列”.
的“生成数列”.
(1)若数列![]() 的“生成数列”是
的“生成数列”是![]() ,求
,求![]() ;
;
(2)若![]() 为偶数,且
为偶数,且![]() 的“生成数列”是
的“生成数列”是![]() ,证明:
,证明:![]() 的“生成数列”是
的“生成数列”是![]() ;
;
(3)若![]() 为奇数,且
为奇数,且![]() 的“生成数列”是
的“生成数列”是![]() ,
,![]() 的“生成数列”是
的“生成数列”是![]() ,…,依次将数列
,…,依次将数列![]() ,
,![]() ,
,![]() ,…的第
,…的第![]() 项取出,构成数列
项取出,构成数列![]() .
.
探究:数列![]() 是否为等比数列,并说明理由.
是否为等比数列,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
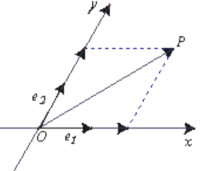
【题目】如图,设![]() 是平面内相交成
是平面内相交成![]() 角的两条数轴 ,
角的两条数轴 ,![]() 分别是
分别是![]() 轴,
轴,![]() 轴正方向同向的单位向量,若向量
轴正方向同向的单位向量,若向量![]() ,则把有序数对
,则把有序数对![]() 叫做向量
叫做向量![]() 在坐标系
在坐标系![]() 中的坐标,假设
中的坐标,假设![]() .
.
(1)计算![]() 的大小;
的大小;
(2)设向量![]() ,若
,若![]() 与
与![]() 共线,求实数
共线,求实数![]() 的值;
的值;
(3)是否存在实数![]() ,使得
,使得![]() 与向量
与向量![]() 垂直,若存在求出
垂直,若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在数列{an}中,a1=2,a2=4,且当n≥2时,an2=an-1an+1,![]() ;
;
(1)求数列{an}的通项公式an;
(2)若bn=(2n-1)an,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目: 来源: 题型:
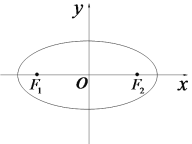
【题目】平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,以
,以![]() 为圆心以3为半径的圆与以
为圆心以3为半径的圆与以![]() 为圆心以1为半径的圆相交,且交点在椭圆
为圆心以1为半径的圆相交,且交点在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 上一动点
上一动点![]() 的直线
的直线![]() ,过F2与x轴垂直的直线记为
,过F2与x轴垂直的直线记为![]() ,右准线记为
,右准线记为![]() ;
;
①设直线![]() 与直线
与直线![]() 相交于点M,直线
相交于点M,直线![]() 与直线
与直线![]() 相交于点N,证明
相交于点N,证明![]() 恒为定值,并求此定值。
恒为定值,并求此定值。
②若连接![]() 并延长与直线
并延长与直线![]() 相交于点Q,椭圆
相交于点Q,椭圆![]() 的右顶点A,设直线PA的斜率为
的右顶点A,设直线PA的斜率为![]() ,直线QA的斜率为
,直线QA的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
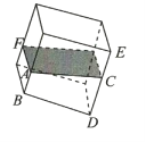
【题目】在一个长方体的容器中,里面装有少量的水,现在将容器绕着其底部的一条棱倾斜.
(1)在倾斜的过程中,水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)在倾斜的过程中,水的形状也不断变化,可以是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底面的一个顶点,上面的第(1)问和第(2)问对不对?
查看答案和解析>>
科目: 来源: 题型:
【题目】国际上钻石的重量计量单位为克拉;已知某种钻石的价值![]() (美元)与其重量
(美元)与其重量![]() (克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为54000美元;
(克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为54000美元;
(1)写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若把一颗钻石切割成重量比为![]() 的两颗钻石,求价值损失的百分率;
的两颗钻石,求价值损失的百分率;
(3)把一颗钻石切割成两颗钻石,若两颗钻石的重量分别为![]() 克拉和
克拉和![]() 克拉,试用你所学的数学知识分析当
克拉,试用你所学的数学知识分析当![]() ,
,![]() 满足何种关系时,价值损失的百分率最大.
满足何种关系时,价值损失的百分率最大.
(注:价值损失的百分率![]() ,在切割过程中重量损耗忽略不计)
,在切割过程中重量损耗忽略不计)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}满足an=logn+1(n+2)(n∈N*)定义使a1a2…ak为整数的数k叫做企盼数,则区间[1,2019]内所有的企盼数的和是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,
(1)若对任意![]() ,
,![]() 且
且![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)在第(1)问求出的实数![]() 的范围内,若存在一个与
的范围内,若存在一个与![]() 有关的负数
有关的负数![]() ,使得对任意
,使得对任意![]() 时
时![]() 恒成立,求
恒成立,求![]() 的最小值及相应的
的最小值及相应的![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com