
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() 右顶点
右顶点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于另外一点
于另外一点![]() ,已知点
,已知点![]() 的纵坐标为
的纵坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点
两点![]() 分别在直线
分别在直线![]() 的上、下方,设四边形
的上、下方,设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市10000名职业中学高三学生参加了一项综合技能测试,从中随机抽取100名学生的测试成绩,制作了以下的测试成绩![]() (满分是184分)的频率分布直方图.
(满分是184分)的频率分布直方图.
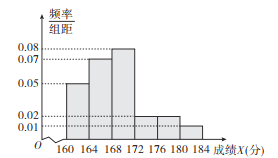
市教育局规定每个学生需要缴考试费100元.某企业根据这100000名职业中学高三学生综合技能测试成绩来招聘员工,划定的招聘录取分数线为172分,且补助已经被录取的学生每个人![]() 元的交通和餐补费.
元的交通和餐补费.
(1)已知甲、乙两名学生的测试成绩分别为168分和170分,求技能测试成绩![]() 的中位数,并对甲、乙的成绩作出客观的评价;
的中位数,并对甲、乙的成绩作出客观的评价;
(2)令![]() 表示每个学生的交费或获得交通和餐补费的代数和,把
表示每个学生的交费或获得交通和餐补费的代数和,把![]() 用
用![]() 的函数来表示,并根据频率分布直方图估计
的函数来表示,并根据频率分布直方图估计![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知三棱锥P﹣ABC中,AC⊥BC,AC=BC=2,PA=PB=PC=3,O是AB中点,E是PB中点.
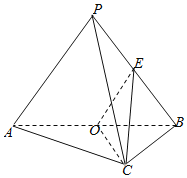
(1)证明:平面PAB⊥平面ABC;
(2)求点B到平面OEC的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于三次函数![]() ,定义
,定义![]() 是
是![]() 的导函数
的导函数![]() 的导函数,经过讨论发现命题:“一定存在实数
的导函数,经过讨论发现命题:“一定存在实数![]() ,使得
,使得![]() 成立”为真,请你根据这一结论判断下列命题:
成立”为真,请你根据这一结论判断下列命题:
①一定存在实数![]() ,使得
,使得![]() 成立;②一定存在实数
成立;②一定存在实数![]() ,使得
,使得![]() 成立;③若
成立;③若![]() ,则
,则![]() ;④若存在实数
;④若存在实数![]() ,且
,且![]() 满足:
满足:![]() ,则函数
,则函数![]() 在
在![]() 上一定单调递增,所有正确的序号是( )
上一定单调递增,所有正确的序号是( )
A. ①② B. ①③ C. ②③ D. ②④
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法:①![]() 越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若
越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若![]() ,则
,则![]() 类比推出,“若
类比推出,“若![]() ,则
,则![]() ;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
A.0B.1C.2D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】已知以点![]() 为圆心的圆C被直线
为圆心的圆C被直线![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆C的标准方程:
(2)求过![]() 与圆C相切的直线方程:
与圆C相切的直线方程:
(3)若Q是直线![]() 上的动点,QR,QS分别切圆C于R,S两点.试问:直线RS是否恒过定点?若是,求出恒过点坐标:若不是,说明理由.
上的动点,QR,QS分别切圆C于R,S两点.试问:直线RS是否恒过定点?若是,求出恒过点坐标:若不是,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在几何体P﹣ABCD中,平面ABCD⊥平面PAB ,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.

(1)求证:EF∥平面PCD;
(2)求直线DP与平面ABCD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com