
科目: 来源: 题型:
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是2019年我国某地区新能源乘用车的前5个月销售量与月份的统计表:
月份代码 | 1 | 2 | 3 | 4 | 5 |
销售量 | 0.5 | 0.6 | 1 | 1.4 | 1.5 |
(1)利用线性相关系数![]() 判断
判断![]() 与
与![]() 的线性相关性,并求出线性回归方程
的线性相关性,并求出线性回归方程
(2)根据线性回归方程预报2019年6月份的销售量约为多少万辆?
参考公式: ,
,![]() ;回归直线:
;回归直线:![]() .
.
 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司推广线下分店,计划在S市的A区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这个x个分店的年收入之和.

(1)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程![]()
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
(参考公式:![]() ,其中
,其中 ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了100名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,按阅读时间分组:第一组[0,5), 第二组[5,10),第三组[10,15),第四组[15,20),第五组[20,25],绘制了频率分布直方图如下图所示。已知第三组的频数是第五组频数的3倍。
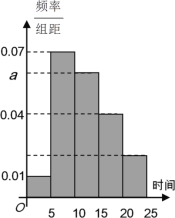
(1)求![]() 的值,并根据频率分布直方图估计该校学生一周课外阅读时间的平均值;
的值,并根据频率分布直方图估计该校学生一周课外阅读时间的平均值;
(2)现从第三、四、五这3组中用分层抽样的方法抽取6人参加校“中华诗词比赛”。经过比赛后,从这6人中随机挑选2人组成该校代表队,求这2人来自不同组别的概率。
查看答案和解析>>
科目: 来源: 题型:
【题目】某文体局为了解“跑团”每月跑步的平均里程,收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图.根据折线图,下列结论正确的是( )

A. 月跑步平均里程的中位数为6月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相对于6月至11月,波动性更小,变化比较平稳
查看答案和解析>>
科目: 来源: 题型:
【题目】四色猜想是近代数学难题之一,四色猜想的内容是:“任何一张地图最多用四种颜色就能使具有共同边界的国家着上不同的颜色”,如图,一张地图被分成了五个区域,每个区域只使用一种颜色,现有4种颜色可供选择(四种颜色不一定用完),则满足四色猜想的不同涂色种数为__________

查看答案和解析>>
科目: 来源: 题型:
【题目】某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.
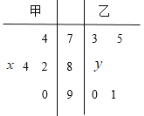
(1)求出x,y的值,且分别求甲、乙两个班中5名学生成绩的方差![]() 、
、![]() ,并根据结
,并根据结
果,你认为应该选派哪一个班的学生参加决赛?
(2)从成绩在85分及以上的学生中随机抽取2名.求至少有1名来自甲班的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题:
①相关指数![]() 越小,则残差平方和越小,模型的拟合效果越好.
越小,则残差平方和越小,模型的拟合效果越好.
②在![]() 的列联表中我们可以通过等高条形图直观判断两个变量是否有关.
的列联表中我们可以通过等高条形图直观判断两个变量是否有关.
③残差点比较均匀地落在水平带状区域内,带状区域越窄,说明模型拟合精度越高.
④两个随机变量相关性越强,则相关系数r越接近1.
其中正确命题的个数为( ).
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】对某两名高三学生连续9次数学测试的成绩(单位:分)进行统计得到如下折线图.下列有关这两名学生数学成绩的分析中,错误的结论是( )


A.甲同学的成绩折线图具有较好的对称性,与正态曲线相近,故而平均成绩为130分
B.根据甲同学成绩折线图中的数据进行统计,估计该同学平均成绩在区间![]() 内
内
C.乙同学的数学成绩与测试次号具有比较明显的线性相关性,且为正相关
D.乙同学在这连续九次测验中的最高分与最低分的差超过40分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com