
科目: 来源: 题型:
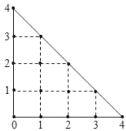
【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收货量![]() (单位:kg)与它的“相近”作物株数
(单位:kg)与它的“相近”作物株数![]() 之间的关系如下表所示:
之间的关系如下表所示:
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(Ⅰ)完成下表,并求所种作物的平均年收获量;
Y | 51 | 48 | 45 | 42 |
频数 | 4 |
(Ⅱ)在所种作物中随机选取一株,求它的年收获量至少为48kg的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动.在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论.若根据欧拉得出的结论,估计10000以内的素数的个数为(素数即质数,
的结论.若根据欧拉得出的结论,估计10000以内的素数的个数为(素数即质数,![]() ,计算结果取整数)
,计算结果取整数)
A. 1089 B. 1086 C. 434 D. 145
查看答案和解析>>
科目: 来源: 题型:
【题目】各国医疗科研机构都在研制某种病毒疫苗,现有G,E,F三个独立的医疗科研机构,它们在一定时期内能研制出疫苗的概率分别是![]() .求:
.求:
(1)他们都研制出疫苗的概率;
(2)他们都失败的概率;
(3)他们能够研制出疫苗的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】若![]() 是一个由数字1,2,3,4,5,6,7,8,9组成的
是一个由数字1,2,3,4,5,6,7,8,9组成的![]() 位正整数,并同时满足如下两个条件:
位正整数,并同时满足如下两个条件:
(1)数字1,2,…,![]() 在
在![]() 中各出现两次;
中各出现两次;
(2)每两个相同的数字![]() 之间恰有
之间恰有![]() 个数字.
个数字.
此时,我们称这样的正整数![]() 为“好数”.例如,当
为“好数”.例如,当![]() 时,
时,![]() 可以是312 132.试确定满足条件的正整数
可以是312 132.试确定满足条件的正整数![]() 的值,并各写出一个相应的好数
的值,并各写出一个相应的好数![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场销售某件商品的经验表明,该商品每日的销量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克)满足关系式
(单位:元/千克)满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为
为常数.已知销售价格为![]() 元/千克时,每日可售出该商品
元/千克时,每日可售出该商品![]() 千克.
千克.
(1)求实数![]() 的值;
的值;
(2)若该商品的成本为![]() 元/千克,试确定销售价格
元/千克,试确定销售价格![]() 的值,使商场每日销售该商品所获得的利润最大,并求出最大值.
的值,使商场每日销售该商品所获得的利润最大,并求出最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了了解某市民众对某项公共政策的态度,在该市随机抽取了50名市民进行调查,作出他们的月收入(单位:百元,范围:![]() )的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
)的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:

月收入 | 赞成的人数 |
| 4 |
| 8 |
| 12 |
| 5 |
| 2 |
| 2 |
(1)求月收入在![]() 内的频率,补全频率分布直方图,并在图中标出相应纵坐标;
内的频率,补全频率分布直方图,并在图中标出相应纵坐标;
(2)若从月收入在![]() 内的被调查者中随机选取2人,求这2人对该项政策都不赞成的概率.
内的被调查者中随机选取2人,求这2人对该项政策都不赞成的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)是否存在实数![]() 、
、![]() ,使得函数
,使得函数![]() 的定义域和值域都是
的定义域和值域都是![]() ?若存在,请求出
?若存在,请求出![]() ,
,![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)若存在实数![]() ,
,![]() ,使得函数
,使得函数![]() 的定义域是
的定义域是![]() ,值域是
,值域是![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】全网传播的融合指数是衡量电视媒体在中国网民中影响力的综合指标,根据相关报道提供的全网传播2018年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 内的概率.
内的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1,2,3,4的四张卡片,现从甲、乙两个盒子中各取出一张卡片,每张卡片被取出的可能性相等.
(1)求取出的两张卡片上标号为相邻整数的概率;
(2)求取出的两张卡片上标号之和能被3整除的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com