
科目: 来源: 题型:
【题目】若四面体![]() 的三组对棱分别相等,即
的三组对棱分别相等,即![]() ,
,![]() ,
,![]() ,给出下列结论:
,给出下列结论:
①四面体![]() 每组对棱相互垂直;
每组对棱相互垂直;
②四面体![]() 每个面的面积相等;
每个面的面积相等;
③从四面体![]() 每个顶点出发的三条棱两两夹角之和大于
每个顶点出发的三条棱两两夹角之和大于![]() 而小于
而小于![]() ;
;
④连接四面体![]() 每组对棱中点的线段相互垂直平分;
每组对棱中点的线段相互垂直平分;
⑤从四面体![]() 每个顶点出发的三条棱的长可作为一个三角形的三边长.
每个顶点出发的三条棱的长可作为一个三角形的三边长.
其中正确结论的个数是( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目: 来源: 题型:
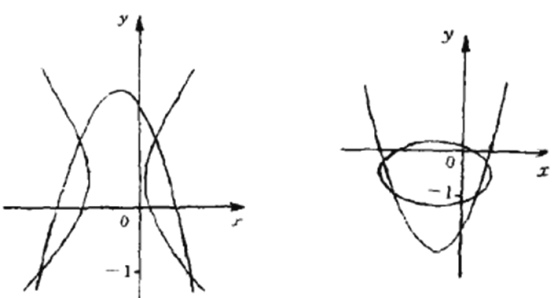
【题目】已知抛物线![]() 与二次曲线
与二次曲线![]() 有4个不同的交点,由下面的草图可以看出,下面三个结论是成立的,请给出证明.
有4个不同的交点,由下面的草图可以看出,下面三个结论是成立的,请给出证明.
(1).两曲线的4个交点中,至少有两个交点位于![]() 轴的下方;
轴的下方;
(2).抛物线![]() 必与
必与![]() 轴有两个不同的交点,记为
轴有两个不同的交点,记为![]() ,
,![]() ,
,![]() ;
;
(3).两曲线的4个交点中,必存在一点![]() ,使
,使![]() .
.
注.对![]() 、
、![]() 、
、![]() 的不同取值会有无数个图形,此处仅就
的不同取值会有无数个图形,此处仅就![]() ,
,![]() 各给出一个示意图,同时也就限制“由图看出”的解答.
各给出一个示意图,同时也就限制“由图看出”的解答.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产了一批高精尖的仪器,为确保仪器的可靠性,工厂安排了一批专家检测仪器的可靠性,毎台仪器被毎位专家评议为“可靠”的概率均为![]() ,且每台仪器是否可靠相互独立.
,且每台仪器是否可靠相互独立.
(1)当![]() ,现抽取4台仪器,安排一位专家进行检测,记检测结果可靠的仪器台数为
,现抽取4台仪器,安排一位专家进行检测,记检测结果可靠的仪器台数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)为进一步提高出厂仪器的可靠性,工厂决定每台仪器都由三位专家进行检测,只有三位专家都检验仪器可靠,则仪器通过检测.若三位专家检测结果都为不可靠,则仪器报废.其余情况,仪器需要回厂返修.拟定每台仪器检测费用为100元,若回厂返修,每台仪器还需要额外花费300元的维修费.现以此方案实施,且抽检仪器为100台,工厂预算3.3万元用于检测和维修,问费用是否有可能会超过预算?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】试确定平面上是否存在满足下述条件的两个不相交的无限点集![]() 、
、![]() :
:
(1)在![]() 中,任何三点不共线,且任何两点的距离至少为1;
中,任何三点不共线,且任何两点的距离至少为1;
(2)任何一个顶点在![]() 中的三角形,其内部均存在一个
中的三角形,其内部均存在一个![]() 中的点,任何一个顶点在
中的点,任何一个顶点在![]() 中的三角形,其内部均存在一个
中的三角形,其内部均存在一个![]() 中的点.
中的点.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.

(Ⅰ)求证:AF∥平面PEC;
(Ⅱ)求证:平面PEC⊥平面PCD.
查看答案和解析>>
科目: 来源: 题型:
【题目】在箱子中有10个小球,其中有3个红球,3个白球,4个黑球.从这10个球中任取3个.求:
(1)取出的3个球中红球的个数![]() 的分布列;
的分布列;
(2)取出的3个球中红球个数多于白球个数的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (α为参数),直线C2的方程为
(α为参数),直线C2的方程为![]() ,以O为极点,x轴的正半轴为极轴建立极坐标系.
,以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1和直线C2的极坐标方程;
(2)若直线C2与曲线C1交于A,B两点,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,椭圆W:![]() 的焦距与椭圆Ω:
的焦距与椭圆Ω:![]() +y2=1的短轴长相等,且W与Ω的长轴长相等,这两个椭圆的在第一象限的交点为A,直线l经过Ω在y轴正半轴上的顶点B且与直线OA(O为坐标原点)垂直,l与Ω的另一个交点为C,l与W交于M,N两点.
+y2=1的短轴长相等,且W与Ω的长轴长相等,这两个椭圆的在第一象限的交点为A,直线l经过Ω在y轴正半轴上的顶点B且与直线OA(O为坐标原点)垂直,l与Ω的另一个交点为C,l与W交于M,N两点.
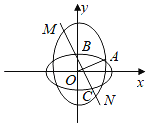
(1)求W的标准方程:
(2)求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com