
【题目】已知![]() ,函数
,函数![]() ,函数
,函数![]() .
.
(1)当函数![]() 图象与
图象与![]() 轴相切时,求实数
轴相切时,求实数![]() 的值;
的值;
(2)若函数![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,讨论函数
时,讨论函数![]() 在区间
在区间![]() 上的零点个数.
上的零点个数.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() 在区间
在区间![]() 有1个零点,当
有1个零点,当![]() 时,
时,![]() 在区间
在区间![]() 内无零点.
内无零点.
【解析】
(1)设切点![]() ,由导数的几何意义为切线的斜率构建方程,求得答案;
,由导数的几何意义为切线的斜率构建方程,求得答案;
(2)结合已知表示函数![]() 的解析式,对其求导,由导函数解析式可知
的解析式,对其求导,由导函数解析式可知![]() 在
在![]() 单调递增,再分类讨论当
单调递增,再分类讨论当![]() ,当
,当![]() ,两种情况下
,两种情况下![]() 的单调性和最值即可;
的单调性和最值即可;
(3)结合已知表示函数![]() 的解析式,对其求导,由导函数解析式可知
的解析式,对其求导,由导函数解析式可知![]() 在
在![]() 单调递减,分类讨论当
单调递减,分类讨论当![]() 时,易证
时,易证![]() ,无零点;当
,无零点;当![]() 时,由不等式性质与单调性易证得有1个零点;当
时,由不等式性质与单调性易证得有1个零点;当![]() 时,由零点的存在性定理可知存在唯一
时,由零点的存在性定理可知存在唯一![]() ,使得
,使得![]() ,再利用导数分析单调性,进而分析出此时无零点.
,再利用导数分析单调性,进而分析出此时无零点.
(1)由题得设切点![]() ,
,![]() ,
,![]()
所以![]() ,
,![]()
![]() ,解得
,解得![]()
![]() ;
;
(2)![]() ,
,
因为![]() 在
在![]() 单调递增,所以
单调递增,所以![]() 在
在![]() 单调递增,
单调递增,
所以![]() .
.
当![]() ,
,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
所以![]() 恒成立,所以
恒成立,所以![]() .
.
当![]() ,
,![]() ,
,
所以![]() ,
,
当![]() ,
,
所以![]() ,使得
,使得![]() ,
,
当![]() ,
,![]() ,
,![]() 在
在![]() 单调递减,
单调递减,
所以![]() 时,
时,![]() ,与
,与![]() 矛盾舍去.
矛盾舍去.
综上 ![]() .
.
(3)![]() ,
,![]() ,
,![]() 在
在![]() 单调递减.
单调递减.
当![]() 时,
时,![]() ,因为
,因为![]() ,
,
所以![]() ,即
,即![]() 在
在![]() 单调递增.
单调递增.
则![]() ,所以
,所以![]() 在区间
在区间![]() 内无零点.
内无零点.
当![]() 时,
时,![]() ,
,
所以![]() ,
,
![]() ,所以存在唯一
,所以存在唯一![]() ,使得
,使得![]() .
.
所以![]() 在区间
在区间![]() 有1个零点.
有1个零点.
当![]() 时,
时,![]()
![]() 在
在![]() 单调递减,
单调递减,
所以存在唯一![]() ,使得
,使得![]() ,
,
当![]() ,
,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
当![]() ,
,![]() ,
,![]() 在
在![]() 单调递减,
单调递减,
所以当![]() 时,
时,![]() 最大值为
最大值为![]() ,
,
代入![]() 得,
得,![]() ,
,
因为![]() ,所以
,所以![]() ,故
,故![]() ,
,
所以![]() ,在
,在![]() 在区间
在区间![]() 内无零点.
内无零点.
综上,当![]() 时,
时,![]() 在区间
在区间![]() 有1个零点,
有1个零点,
当![]() 时,
时,![]() 在区间
在区间![]() 内无零点.
内无零点.


科目:高中数学 来源: 题型:
【题目】设函数![]() 的最小正周期为
的最小正周期为![]() ,且其图象关于直线
,且其图象关于直线![]() 对称,则在下面结论中正确的个数是( )
对称,则在下面结论中正确的个数是( )
①图象关于点![]() 对称;
对称;
②图象关于点![]() 对称;
对称;
③在![]() 上是增函数;
上是增函数;
④在![]() 上是增函数;
上是增函数;
⑤由![]() 可得
可得![]() 必是
必是![]() 的整数倍.
的整数倍.
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的PK赛,![]() 两队各由4名选手组成,每局两队各派一名选手PK,比赛四局.除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为
两队各由4名选手组成,每局两队各派一名选手PK,比赛四局.除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为![]() ,且各局比赛结果相互独立,比赛结束时A队的得分高于B队的得分的概率为( )
,且各局比赛结果相互独立,比赛结束时A队的得分高于B队的得分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小店每天以每份5元的价格从食品厂购进若干份食品,然后以每份10元的价格出售.如果当天卖不完,剩下的食品还可以每份1元的价格退回食品厂处理.
(Ⅰ)若小店一天购进16份,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:份,
(单位:份,![]() )的函数解析式;
)的函数解析式;
(Ⅱ)小店记录了100天这种食品的日需求量(单位:份),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)小店一天购进16份这种食品,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列及数学期望;
的分布列及数学期望;
(ii)以小店当天利润的期望值为决策依据,你认为一天应购进食品16份还是17份?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (α为参数),直线C2的方程为
(α为参数),直线C2的方程为![]() ,以O为极点,x轴的正半轴为极轴建立极坐标系.
,以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1和直线C2的极坐标方程;
(2)若直线C2与曲线C1交于A,B两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的偶函数,且对任意的
上的偶函数,且对任意的![]() 恒有
恒有![]() ,已知当
,已知当![]() 时,
时,![]() ,则
,则
①![]() 是函数
是函数![]() 的一个周期;
的一个周期;
②函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
③函数![]() 的最大值是
的最大值是![]() ,最小值是
,最小值是![]() ;
;
④![]() 是函数
是函数![]() 的一个对称轴;
的一个对称轴;
其中所有正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD
为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD![]() 平面PBC=
平面PBC=![]() .
.
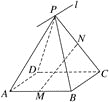
(1)求证:BC∥![]() ;
;
(2)MN与平面PAD是否平行?试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数![]() .在平面直角坐标系
.在平面直角坐标系![]() 中,已知点
中,已知点![]() ,直线
,直线![]() :
:![]() ,曲线
,曲线![]() :
:![]() .
.![]() 与
与![]() 轴交于点
轴交于点![]() 、与
、与![]() 交于点
交于点![]() .
.![]() 、
、![]() 分别是曲线
分别是曲线![]() 与线段
与线段![]() 上的动点.
上的动点.
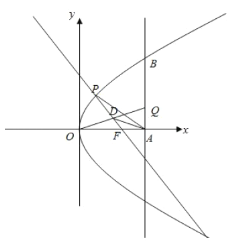
(1)用![]() 表示点
表示点![]() 到点
到点![]() 距离;
距离;
(2)设![]() ,
,![]() ,线段
,线段![]() 的中点在直线
的中点在直线![]() ,求
,求![]() 的面积;
的面积;
(3)设![]() ,是否存在以
,是否存在以![]() 、
、![]() 为邻边的矩形
为邻边的矩形![]() ,使得点
,使得点![]() 在
在![]() 上?若存在,求点
上?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在R上是增函数,求实数a的取值范围;
在R上是增函数,求实数a的取值范围;
(2)求所有的实数a,使得对任意![]() 时,函数
时,函数![]() 的图象恒在函数
的图象恒在函数![]() 图象的下方;
图象的下方;
(3)若存在![]() ,使得关于x的方程
,使得关于x的方程![]() 有三个不相等的实数根,求实数t的取值范围.
有三个不相等的实数根,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com