
【题目】如图所示,![]() 为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD
为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD![]() 平面PBC=
平面PBC=![]() .
.
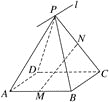
(1)求证:BC∥![]() ;
;
(2)MN与平面PAD是否平行?试证明你的结论.
【答案】(1)见解析;(2)见解析
【解析】
试题证明线线平行的方法;1,向量法,2.垂直于同一平面的两条直线平行,3平行于同一直线的两条直线平行,4一个平面与另外两个平行平面相交,那么两条交线也平行。线面平行,1平面外的一条直线与平面内的一条直线平行,则这条直线与这个平面平行,2若一条直线与一个平面同时平行于另一个平面且这条直线不属于这个平面,则这条直线与这个平面平行,3若一条直线与两平行平面中的一个平行,则这条直线与另一个平面平行,4,最好用的还是向量法。
试题解析:(1)证明 因为BC∥AD,AD平面PAD,
BC平面PAD,所以BC∥平面PAD.
又平面PAD∩平面PBC=l,BC平面PBC,所以BC∥l.
(2)解 MN∥平面PAD.证明如下:
如图所示,取PD中点E,连结AE,EN.
又∵N为PC的中点,∴![]()
又∵![]()
∴![]()
即四边形AMNE为平行四边形.
∴AE∥MN,又MN平面PAD,AE平面PAD
.∴MN∥平面PAD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】工厂需要围建一个面积为512![]() 的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁.我们知道,砌起的新墙的总长度
的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁.我们知道,砌起的新墙的总长度![]() (单位:
(单位: ![]() )是利用原有墙壁长度
)是利用原有墙壁长度![]() (单位:
(单位: ![]() )的函数.
)的函数.
(1)写出![]() 关于
关于![]() 的函数解析式,确定
的函数解析式,确定![]() 的取值范围.
的取值范围.
(2)堆料场的长、宽之比为多少时,需要砌起的新墙用的材料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=e﹣x(lnx﹣2k)(k为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与y轴垂直.
(1)求f(x)的单调区间;
(2)设 ![]() ,对任意x>0,证明:(x+1)g(x)<ex+ex﹣2 .
,对任意x>0,证明:(x+1)g(x)<ex+ex﹣2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面为正方形的四棱锥P-ABCD中,侧棱PD⊥底面ABCD,PD=DC,点E是线段PC的中点.

(1)求异面直线AP与BE所成角的大小;
(2)若点F在线段PB上,使得二面角F-DE-B的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mex+x2+nx,{x|f(x)=0}={x|f(f(x))=0}≠,则m+n的取值范围为( )
A.(0,4)
B.[0,4)
C.[0,4]
D.(4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
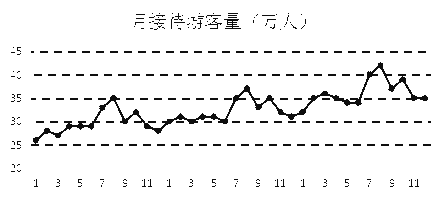
2014年 2015年 2016年
根据该折线图,下列结论错误的是( )
A. 年接待游客量逐年增加
B. 月接待游客量逐月增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD﹣A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法:

(1)平面MENF⊥平面BDD′B′;
(2)当且仅当x=![]() 时,四边形MENF的面积最小;
时,四边形MENF的面积最小;
(3)四边形MENF周长L=f(x),x∈[0,1]是单调函数;
(4)四棱锥C′﹣MENF的体积V=h(x)为常函数,以上说法中正确的为( )
A. (2)(3) B. (1)(3)(4) C. (1)(2)(4) D. (1)(2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com