练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数的最小正周期为，且其图象关于直线对称，则在下面结论中正确的个数是（ ）

    ①图象关于点对称；

    ②图象关于点对称；

    ③在上是增函数；

    ④在上是增函数；

    ⑤由可得必是的整数倍.

    A.4B.3C.2D.1

    【答案】C

    【解析】

    根据最小正周期及对称轴，可求得函数解析式，由正弦函数的图象与性质即可判断选项.

    因为函数的最小正周期为，

    则，

    所以

    函数图象关于直线对称，

    则

    则

    因为，所以当时得，

    即，

    由正弦函数的图像与性质可知，对称中心为，解得

    当时，所以对称中心为，故②正确，①错误；

    由正弦函数的图像与性质可知，当时，函数单增，

    解得，当时，单调递增区间为

    因为所以④正确，③错误；

    因为最小正周期为，若，可得必是的整数倍，所以⑤错误.

    综上可知，正确的为②④，

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了调查患胃病是否与生活不规律有关，在患胃病与生活不规律这两个分类变量的计算中，下列说法正确的是（ ）

    A. 越大，“患胃病与生活不规律没有关系”的可信程度越大.

    B. 越大，“患胃病与生活不规律有关系”的可信程度越小.

    C.若计算得 ，经查临界值表知 ，则在 个生活不规律的人中必有 人患胃病.

    D.从统计量中得知有 的把握认为患胃病与生活不规律有关，是指有 的可能性使得推断出现错误.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】上饶市在某次高三适应性考试中对数学成绩数据统计显示，全市10000名学生的成绩近似服从正态分布，现某校随机抽取了50名学生的数学成绩分析，结果这50名学生的成绩全部介于85分到145分之间，现将结果按如下方式分为6组，第一组，第二组，…，第六组，得到如图所示的频率分布直方图：

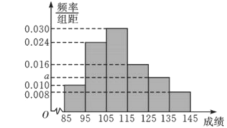
    （1）试由样本频率分布直方图估计该校数学成绩的平均分数；

    （2）若从这50名学生中成绩在125分（含125分）以上的同学中任意抽取3人，该3人在全市前13名的人数记为，求的概率.

    附：若，则，，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了提高学生的身体素质，某校高一、高二两个年级共名学生同时参与了“我运动，我健康，我快乐”的跳绳、踢毽等系列体育健身活动.为了了解学生的运动状况，采用分层抽样的方法从高一、高二两个年级的学生中分别抽取名和名学生进行测试.下表是高二年级的名学生的测试数据（单位：个/分钟）：

    学生编号

    1

    2

    3

    4

    5

    跳绳个数

    179

    181

    168

    177

    183

    踢毽个数

    85

    78

    79

    72

    80

    （1）求高一、高二两个年级各有多少人？

    （2）设某学生跳绳个/分钟，踢毽个/分钟.当，且时，称该学生为“运动达人”.

    ①从高二年级的学生中任选一人，试估计该学生为“运动达人”的概率；

    ②从高二年级抽出的上述名学生中，随机抽取人，求抽取的名学生中为“span>运动达人”的人数的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）判断的单调性，并证明之；

    （2）若存在实数，，使得函数在区间上的值域为，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量， ，设函数，且的图象过点和点.

    （Ⅰ）求的值；

    （Ⅱ）将的图象向左平移（）个单位后得到函数的图象.若的图象上各最高点到点的距离的最小值为1，求的单调增区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率与双曲线的离心率互为倒数，分别为椭圆的左、右顶点，且.

    （1）求椭圆的方程；

    （2）已知过左顶点的直线与椭圆另交于点，与轴交于点，在平面内是否存在一定点，使得恒成立？若存在，求出该点的坐标，并求面积的最大值；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足：①（）；②当（）时，；③当（）时，，记数列的前项和为.

    （1）求，，的值；

    （2）若，求的最小值；

    （3）求证：的充要条件是（）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，函数，函数．

    （1）当函数图象与轴相切时，求实数的值；

    （2）若函数对恒成立，求实数的取值范围；

    （3）当时，讨论函数在区间上的零点个数．

    查看答案和解析>>

    同步练习册答案