
����Ŀ��Ϊ�����ѧ�����������ʣ�ijУ��һ���߶������꼶��![]() ��ѧ��ͬʱ�����������˶����ҽ������ҿ���������������릵�ϵ�����������.Ϊ���˽�ѧ�����˶�״�������÷ֲ�����ķ����Ӹ�һ���߶������꼶��ѧ���зֱ��ȡ
��ѧ��ͬʱ�����������˶����ҽ������ҿ���������������릵�ϵ�����������.Ϊ���˽�ѧ�����˶�״�������÷ֲ�����ķ����Ӹ�һ���߶������꼶��ѧ���зֱ��ȡ![]() ����
����![]() ��ѧ�����в���.�±��Ǹ߶��꼶��
��ѧ�����в���.�±��Ǹ߶��꼶��![]() ��ѧ���IJ������ݣ���λ����/���ӣ���
��ѧ���IJ������ݣ���λ����/���ӣ���
ѧ����� | 1 | 2 | 3 | 4 | 5 |
�������� | 179 | 181 | 168 | 177 | 183 |
��릸��� | 85 | 78 | 79 | 72 | 80 |
��1�����һ���߶������꼶���ж����ˣ�
��2����ijѧ������![]() ��/���ӣ����
��/���ӣ����![]() ��/����.��
��/����.��![]() ����
����![]() ʱ���Ƹ�ѧ��Ϊ���˶�������.
ʱ���Ƹ�ѧ��Ϊ���˶�������.
�ٴӸ߶��꼶��ѧ������ѡһ�ˣ��Թ��Ƹ�ѧ��Ϊ���˶��������ĸ��ʣ�
�ڴӸ߶��꼶���������![]() ��ѧ���У������ȡ
��ѧ���У������ȡ![]() �ˣ����ȡ��
�ˣ����ȡ��![]() ��ѧ����Ϊ��span>�˶�������������
��ѧ����Ϊ��span>�˶�������������![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
���𰸡���1����һ�꼶��![]() �ˣ��߶��꼶��
�ˣ��߶��꼶��![]() �ˣ���2����
�ˣ���2����![]() ���ڼ�������
���ڼ�������![]()
��������
��1�����ݷֲ�������ص�ֱ������𰸣�
��2�����ɱ���֪���Ӹ߶���ȡ��ѧ�������˶���������3�ˣ�������������
�������֪![]() �����п���ȡֵΪ
�����п���ȡֵΪ![]() ��ͨ�������г��ֲ��У������ѧ��������.
��ͨ�������г��ֲ��У������ѧ��������.
��1�����һ�꼶��![]() �ˣ��߶��꼶��
�ˣ��߶��꼶��![]() ��.
��.
���÷ֲ��������![]() ��
��![]() �����Ը�һ�꼶��
�����Ը�һ�꼶��![]() �ˣ��߶��꼶��
�ˣ��߶��꼶��![]() ��.
��.
��2�����ϱ���֪���Ӹ߶���ȡ��![]() ��ѧ���У����Ϊ
��ѧ���У����Ϊ![]() ��ѧ�������˶�������.�ʴӸ߶��꼶��ѧ������ѡһ�ˣ���ѧ��Ϊ���˶��������ĸ��ʹ���Ϊ
��ѧ�������˶�������.�ʴӸ߶��꼶��ѧ������ѡһ�ˣ���ѧ��Ϊ���˶��������ĸ��ʹ���Ϊ![]() ��
��
��![]() �����п���ȡֵΪ
�����п���ȡֵΪ![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 1 | 2 | 3 |
|
|
|
|
��![]() ������
������![]() .
.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1������y��f��x���ĵ������䣻
��2��������x�ʣ�0��+�ޣ�����![]() ����������m��ȡֵ��Χ��
����������m��ȡֵ��Χ��
��3����g��x����f��x��+x��n��3����m��1ʱ������g��x��������[e��1��e]����������㣬��ʵ��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��![]() �ǵȱ������Σ�D.E�ֱ���BC.AC�����㣬��
�ǵȱ������Σ�D.E�ֱ���BC.AC�����㣬��![]() ��
��![]() ��AD���ڵ�H������CH.
��AD���ڵ�H������CH.
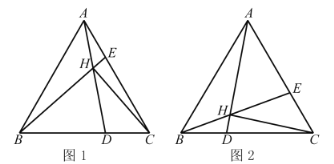
��1����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��2����ͼ2����![]() ʱ��
ʱ��![]() __________��
__________��![]() __________.
__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
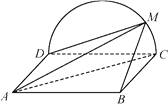
����Ŀ����ͼ���߳�Ϊ2��������![]() ���ڵ�ƽ�����Բ��
���ڵ�ƽ�����Բ��![]() ����ƽ�洹ֱ��
����ƽ�洹ֱ��![]() ��
��![]() ������
������![]() ��
��![]() �ĵ㣮
�ĵ㣮
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ʱ������
������ʱ������![]() ����
����![]() ���ɶ���ǵ�����ֵ��
���ɶ���ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Ȼ��![]() ��20�����������ӣ�����1�ͱ����������Ǵ�С�������μ���
��20�����������ӣ�����1�ͱ����������Ǵ�С�������μ���![]() ��
��![]() ��
��![]() ������
������![]() �������Ϊ
�������Ϊ![]() ������Ϊ
������Ϊ![]() ������Ȼ��
������Ȼ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һЩѡ�ֲμ���ѧ������������Щѡ�ֻ�����ʶ����Щѡ�ֻ����ʶ�����κ���������ʶ��ѡ�ֶ�ǡ��������ͬ�����ˣ���![]() ��
��![]() ��ʶ����û�й�ͬ�����ˣ���֤��
��ʶ����û�й�ͬ�����ˣ���֤��![]() ��
��![]() ��ʶ������һ���࣮
��ʶ������һ���࣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ����С������Ϊ
����С������Ϊ![]() ������ͼ�����ֱ��
������ͼ�����ֱ��![]() �Գƣ����������������ȷ�ĸ����ǣ� ��
�Գƣ����������������ȷ�ĸ����ǣ� ��
��ͼ����ڵ�![]() �Գƣ�
�Գƣ�
��ͼ����ڵ�![]() �Գƣ�
�Գƣ�
����![]() ������������
������������
����![]() ������������
������������
����![]() �ɵ�
�ɵ�![]() ����
����![]() ��������.
��������.
A.4B.3C.2D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ᰲ���˷ֱ�������Ϊ��1�š���2�š���3�š������������ȿ������˳��ǰ���Ƶ�Ӽα���ij�α�ͻ�����룬������ֳ˳�����������һ����������һ���������ڶ������ij���Ŵ��ڵ�һ�����ij���ţ��ͳ����˳����������������������������ֱ�ӳ�����һ�������Ƿ���һ�뷽����������3�š����ĸ��ʷֱ�ΪP1��P2������ ��
A. P1P2��![]() B. P1��P2��
B. P1��P2��![]() C. P1+P2��
C. P1+P2��![]() D. P1��P2
D. P1��P2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС��ÿ����ÿ��5Ԫ�ļ۸��ʳƷ���������ɷ�ʳƷ��Ȼ����ÿ��10Ԫ�ļ۸����.������������꣬ʣ�µ�ʳƷ������ÿ��1Ԫ�ļ۸��˻�ʳƷ������.
(��)��С��һ�칺��16�ݣ����������![]() ����λ��Ԫ�����ڵ���������
����λ��Ԫ�����ڵ���������![]() ����λ���ݣ�
����λ���ݣ�![]() ���ĺ�������ʽ��
���ĺ�������ʽ��
(��)С���¼��100������ʳƷ��������������λ���ݣ����������±���
�������� | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Ƶ�� | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
��100���¼�ĸ���������Ƶ����Ϊ�������������ĸ���.
(i)С��һ�칺��16������ʳƷ��![]() ��ʾ���������λ��Ԫ������
��ʾ���������λ��Ԫ������![]() �ķֲ��м���ѧ������
�ķֲ��м���ѧ������
(ii)��С�굱�����������ֵΪ�������ݣ�����Ϊһ��Ӧ����ʳƷ16�ݻ���17�ݣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com