【题目】为了调查患胃病是否与生活不规律有关，在患胃病与生活不规律这两个分类变量的计算中，下列说法正确的是（ ）
A.
越大，“患胃病与生活不规律没有关系”的可信程度越大.
B. 越大，“患胃病与生活不规律有关系”的可信程度越小.
C.若计算得
，经查临界值表知
，则在
个生活不规律的人中必有
人患胃病.
D.从统计量中得知有
的把握认为患胃病与生活不规律有关，是指有
的可能性使得推断出现错误.
单元加期末复习先锋大考卷系列答案
出彩同步大试卷系列答案科目：高中数学 来源： 题型：
【题目】设
.若满射
，满足：对任意的
，
，则称
为“和谐函数”.记 
，
.设“和谐映射”为满足条件：存在正整数
，使得（1）当
时，若
，
，则
；（2）若 ，，则
，求的最大可能值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知集合
，其中
，
是函数
定义城内任意不相等的两个实数.
（1）若
，同时
，求证：
；
（2）判断
是否在集合A中，并说明理由；
（3）设函数的定义域为B，函数的值域为C.函数满足以下3个条件：
①，②
，③
.试确定一个满足以上3个条件的函数要对满足的条件进行说明）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）求函数y＝f（x）的单调区间；
（2）若对于x∈（0，+∞）都有
成立，试求m的取值范围；
（3）记g（x）＝f（x）+x﹣n﹣3．当m＝1时，函数g（x）在区间[e﹣1，e]上有两个零点，求实数n的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着西部大开发的深入，西南地区的大学越来越受到广大考生的青睐,下表是西南地区某大学近五年的录取平均分高于省一本线分值对比表：
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
录取平均分高于省一本线分值 | 28 | 34 | 41 | 47 | 50 |
（1）根据上表数据可知，
与
之间存在线性相关关系，求关于的线性回归方程；
（2）假设2020年该省一本线为520分，利用（1）中求出的回归方程预测2020年该大学录取平均分.
参考公式：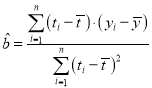
，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂有一个容量为300吨的水塔，每天从早上6时起到晚上10时止供应该厂的生产和生活用水.已知该厂生活用水为每小时10吨，生产用水量
（吨）与时间
（单位：小时，且规定早上6时
）的函数关系式为：
，水塔的进水量分为10级，第一级每小时进水10吨，以后每提高一级，每小时进水量就增加10吨.若某天水塔原有水100吨，在开始供水的同时打开进水管.
（1）若进水量选择为
级，水塔中剩余水量为
吨，试写出与的函数关系式；
（2）如何选择进水量，既能始终保证该厂的用水（水塔中水不空）又不会使水溢出？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，
是等边三角形，D.E分别是BC.AC上两点，且
，
与AD交于点H，链接CH.
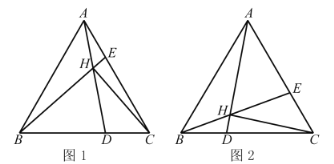
（1）当
时，求
的值；
（2）如图2，当
时，
__________；
__________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
的最小正周期为
，且其图象关于直线
对称，则在下面结论中正确的个数是（ ）
①图象关于点
对称；
②图象关于点
对称；
③在
上是增函数；
④在
上是增函数；
⑤由
可得
必是的整数倍.
A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
