【题目】函数的部分图象如图所示，则下列叙述正确的是( )

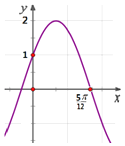
A.函数的图象可由的图象向左平移个单位得到

B.函数的图象关于直线对称

C.函数在区间上是单调递增的

D.函数图象的对称中心为

【题目】已知函数．

（1）讨论的单调性；

（2）若，直线与曲线和曲线都相切，切点分别为，，求证：．

(1)求函数f(x)的解析式；

(2) 令g(x)＝(2－2m)x－f(x)．

① 若函数g(x)在x∈[0，2]上是单调函数，求实数m的取值范围；

② 求函数g(x)在x∈[0，2]上的最小值．

【题目】如图，四棱锥中，平面底面ABCD，是等边三角形，底面ABCD为梯形，且，，．

Ⅰ证明：；

Ⅱ求A到平面PBD的距离．

【题目】年月以来，湖北省武汉市持续开展流感及相关疾病监测，发现多起病毒性肺炎病例，均诊断为病毒性肺炎肺部感染，后被命名为新型冠状病毒肺炎（CoronaVirusDisease2019，COVID-19），简称“新冠肺炎”，下图是年月日至月日累计确诊人数随时间变化的散点图．

为了预测在未采取强力措施下，后期的累计确诊人数，建立了累计确诊人数与时间变量的两个回归模型，根据月日至月日的数据（时间变量的值依次，，…，）建立模型和．

参考数据：其中，．

（1）根据散点图判断，和哪一个适宜作为累计确诊人数与时间变量的回归方程类型？（给出判断即可，不必说明理由）；

（2）根据（1）的判断结果及附表中数据，建立关于的回归方程；

（3）以下是月日至月日累计确诊人数的真实数据，根据（2）的结果回答下列问题：

（i）当月日至月日这天的误差（模型预测数据与真实数据差值的绝对值与真实数据的比值）都小于则认为模型可靠，请判断（2）的回归方程是否可靠？

（ii）年月日在人民政府的强力领导下，全国人民共同取了强力的预防“新冠肺炎”的措施，若采取措施天后，真实数据明显低于预测数据，则认为防护措施有效，请判断预防措施是否有效？并说明理由.

附：对于一组数据，，……，，其回归直线的斜率和截距的最小二乘估计分别为：，．

【题目】在四棱锥P-ABCD中，底面ABCD为直角梯形，，，，，且平面平面ABCD.

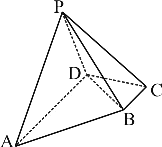
（1）求证：；

（2）在线段PA上是否存在一点M，使二面角M-BC-D的大小为？若存在，求出的值；若不存在，请说明理由.

【题目】已知函数.

（1）求函数的单调区间；

（2）设函数， ， 为自然对数的底数.当时，若， ，不等式成立，求的最大值.

【题目】为了解中学生课外阅读情况，现从某中学随机抽取名学生，收集了他们一年内的课外阅读量（单位：本）等数据，以下是根据数据绘制的统计图表的一部分.

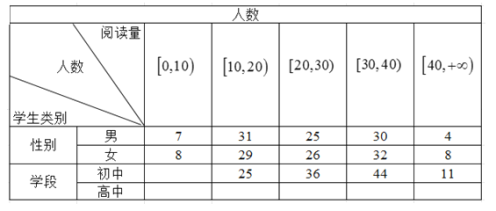
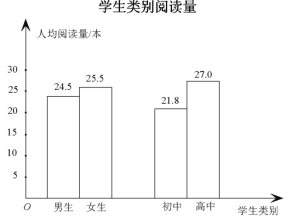
下面有四个推断：

①这名学生阅读量的平均数可能是本；

②这名学生阅读量的分位数在区间内；

③这名学生中的初中生阅读量的中位数一定在区间内；

④这名学生中的初中生阅读量的分位数可能在区间内.

所有合理推断的序号是________.

【题目】甜皮鸭，乐山人称卤鸭子，也称嘉州甜皮鸭，是乐山著名美食，起源于乐山市夹江县木城古镇，每年吸引成千上万的外地人前来品尝.某商家生产卤鸭子，每公斤鸭子的成本为元，加工费为元（为常数），且，设该商家每公斤卤鸭子的售价为元（），日销售量（单位：公斤），且（为自然对数的底数）.根据市场调查，当每公斤卤鸭子的出售价为元时，日销售量为公斤.

（1）求该商家的每日利润元与每公斤卤鸭子的出售价元的函数关系式；

（2）若，当每公斤卤鸭子的出售价为多少元时，该商家的利润最大，并求出利润的最大值．

【题目】如图，在四棱锥中，底面为平行四边形，已知，，于.

（1）求证：；

（2）若平面平面，且，求二面角的余弦值.