
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 都相切,切点分别为
都相切,切点分别为![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)分类讨论,详见解析;(2)详见解析.
【解析】
(1)首先写出函数![]() 定义域为
定义域为![]() ,求得
,求得![]() ,对
,对![]() 的范围进行讨论,从而确定出
的范围进行讨论,从而确定出![]() 的符号,确定出函数
的符号,确定出函数![]() 的单调性;
的单调性;
(2)可以从两个角度去分析,方法一是根据导数的几何意义,写出直线![]() 的方程为
的方程为![]() ,即
,即![]() ,也可以写成
,也可以写成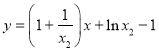 ,根据两条直线是同一条直线,得到
,根据两条直线是同一条直线,得到![]() ,且
,且![]() ,对式子进行整理可以得到
,对式子进行整理可以得到![]() ,构造函数
,构造函数![]() ,利用导数研究该函数的单调性及最值,从而可以证得结果;方法二是根据两条切线的斜率想的得到
,利用导数研究该函数的单调性及最值,从而可以证得结果;方法二是根据两条切线的斜率想的得到 ,进一步可以得到
,进一步可以得到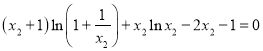 ,构造函数
,构造函数![]() ,利用导数研究该函数的单调性及最值得到结果.
,利用导数研究该函数的单调性及最值得到结果.
(1)![]() 定义域为
定义域为![]() ,
,
因为![]() ,
,
若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
若![]() ,则当
,则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)证法一:
证明:对于曲线![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
即![]() ,即
,即![]() ①.
①.
对于曲线![]() ,因为
,因为![]() ,所以
,所以![]()
所以![]() ,
,
直线![]() 的方程为
的方程为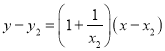 ,
,
即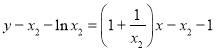 ,即
,即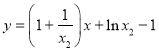 ②.
②.
因为①与②表示同一条直线,所以![]() ③,
③,
且![]() ④,
④,
④÷③,得![]() ,
,
所以![]() .
.
令![]() ,
,
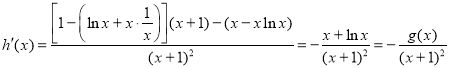 ,
,
由(1)知,![]() 在
在![]() 单调递增又
单调递增又![]()
![]() ∴
∴![]()
![]() 有唯一零点
有唯一零点![]() ,
,
且当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
所以![]() ,
,
又![]() ,即
,即![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() .
.
证法二:
证明:因为![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以直线![]() 的斜率为
的斜率为![]() ,
,
所以![]() ,所以
,所以 ,
,
又因为 ,
,
所以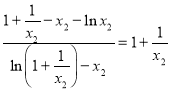 ,
,
所以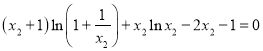 ,
,
令![]() ,
,
所以![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
又因为![]() ,
,![]() ,
,
所以存在![]() ,使得
,使得![]() ,
,
且当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
因为![]() ,所以
,所以![]() 在
在![]() 递减,
递减,
所以当![]() 时,
时, ,
,
所以![]() 在
在![]() 内无零点,
内无零点,
因为![]() 是
是![]() 的零点且
的零点且![]() ,所以
,所以![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,其左焦点到点
,其左焦点到点![]() 的距离为
的距离为![]() ,不过原点O的直线
,不过原点O的直线![]() 与C交于A,B两点,且线段AB被直线OP平分.
与C交于A,B两点,且线段AB被直线OP平分.
(1)求椭圆C的方程;
(2)求k的值;
(3)求![]() 面积取最大值时直线l的方程.
面积取最大值时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 sin(x+![]() )。
)。
(1)若点P(1,-![]() )在角
)在角![]() 的终边上,求:cos
的终边上,求:cos![]() 和f(
和f(![]() -
-![]() )的值;
)的值;
(2)若x![]() [
[![]() ,
, ![]() ],求f(x)的值域。
],求f(x)的值域。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出![]() 盒该产品获利润
盒该产品获利润![]() 元,未售出的产品,每盒亏损
元,未售出的产品,每盒亏损![]() 元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了
元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了![]() 盒该产品,以
盒该产品,以![]() (单位:盒,
(单位:盒,![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量,![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
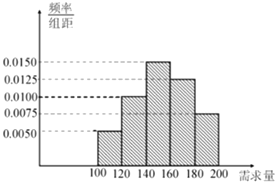
(1)根据直方图估计这个开学季内市场需求量![]() 的众数和平均数(同一组中的数据用该组区间的中点值为代表);
的众数和平均数(同一组中的数据用该组区间的中点值为代表);
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,三棱锥![]() 的体积是18,求
的体积是18,求![]() 点到平面
点到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如表:
损坏餐椅数 | 未损坏餐椅数 | 总计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总计 | 80 | 320 | 400 |
![]() 求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
![]() 请说明是否有
请说明是否有![]() 以上的把握认为损毁餐椅数量与学习雷锋精神
以上的把握认为损毁餐椅数量与学习雷锋精神
有关?![]() 参考公式:
参考公式:![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小陈同学进行三次定点投篮测试,已知第一次投篮命中的概率为![]() ,第二次投篮命中的概率为
,第二次投篮命中的概率为![]() ,前两次投篮是否命中相互之间没有影响.第三次投篮受到前两次结果的影响,如果前两次投篮至少命中一次,则第三次投篮命中的概率为
,前两次投篮是否命中相互之间没有影响.第三次投篮受到前两次结果的影响,如果前两次投篮至少命中一次,则第三次投篮命中的概率为![]() ,否则为
,否则为![]() .
.
(1)求小陈同学三次投篮至少命中一次的概率;
(2)记小陈同学三次投篮命中的次数为随机变量![]() ,求
,求![]() 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
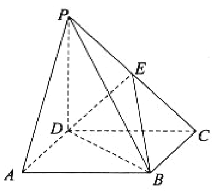
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com