
科目: 来源: 题型:
【题目】乒乓球赛规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换,每次发球,胜方得1分,负方得0分。设在甲、乙的比赛中,每次发球,甲发球得1分的概率为![]() ,乙发球得1分的概率为
,乙发球得1分的概率为![]() ,各次发球的胜负结果相互独立,甲、乙的一局比赛中,甲先发球.则开始第4次发球时,甲、乙的比分为1比2的概率为________.
,各次发球的胜负结果相互独立,甲、乙的一局比赛中,甲先发球.则开始第4次发球时,甲、乙的比分为1比2的概率为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,PA垂直于以AB为直径的圆所在平面,C为圆上异于A,B的任意一点,![]() 垂足为E,点F是PB上一点,则下列判断中不正确的是( )﹒
垂足为E,点F是PB上一点,则下列判断中不正确的是( )﹒
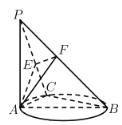
A.![]() 平面PACB.
平面PACB.![]() C.
C.![]() D.平面
D.平面![]() 平面PBC
平面PBC
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点是
的左、右焦点是![]() ,左右顶点是
,左右顶点是![]() ,离心率是
,离心率是![]() ,过
,过![]() 的直线与椭圆交于两点P、Q(不是左、右顶点),且
的直线与椭圆交于两点P、Q(不是左、右顶点),且![]() 的周长是
的周长是![]() ,
,
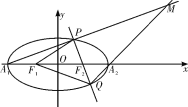
直线![]() 与
与![]() 交于点M.
交于点M.
(1)求椭圆的方程;
(2)(ⅰ)求证直线![]() 与
与![]() 交点M在一条定直线l上;
交点M在一条定直线l上;
(ⅱ)N是定直线l上的一点,且PN平行于x轴,证明:![]() 是定值.
是定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD,AB=![]() AD,E是线段PD上的点,F是线段AB上的点,
AD,E是线段PD上的点,F是线段AB上的点,
且![]() .
.
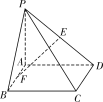
(1)证明:EF∥平面PBC;
(2)是否存在实数λ,使得异面直线EF与CD所成角为60°?若存在,试求出λ的值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C:y2=4x与椭圆E:![]() 1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|
1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|![]() .
.
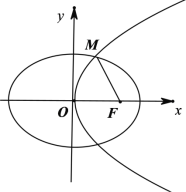
(1)求椭圆E的标准方程;
(2)过点P(1,![]() )的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
)的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正三棱锥![]() ,一个正三棱柱的一个底面的三个顶点在正三棱锥的三条侧棱上,另一底面在正三棱锥的底面上,若正三棱锥的高为15,底面边长为12,内接正三棱柱的侧面积为120.
,一个正三棱柱的一个底面的三个顶点在正三棱锥的三条侧棱上,另一底面在正三棱锥的底面上,若正三棱锥的高为15,底面边长为12,内接正三棱柱的侧面积为120.
(1)求三棱柱的高;
(2)求棱柱的上底面截棱锥所得的小棱锥与原棱锥的侧面积之比.
查看答案和解析>>
科目: 来源: 题型:
【题目】越接近高考学生焦虑程度越强,四个高三学生中大约有一个有焦虑症,经有关机构调查,得出距离高考周数与焦虑程度对应的正常值变化情况如下表:
周数x | 6 | 5 | 4 | 3 | 2 | 1 |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
(1)作出散点图:

(2)根据上表数据用最小二乘法求出y关于x的线性回归方程 (精确到0.01);
(3)根据经验,观测值为正常值的0.85~1.06为正常,若1.06~1.12为轻度焦虑,1.12~1.20为中度焦虑,1.20及其以上为重度焦虑,若为中度焦虑及其以上,则要进行心理疏导,若一个学生在距高考第二周时观测值为100,则该学生是否需要进行心理疏导?
(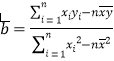 ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com