
科目: 来源: 题型:
【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
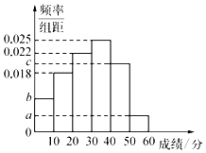
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: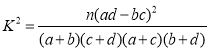 ,其中
,其中![]() .
.
| .15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y(万元)的几组对照数据:
x(年) | 2 | 3 | 4 | 5 | 6 |
y(万元) | 1 | 2.5 | 3 | 4 | 4.5 |
(1)若知道y对x呈线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?
参考公式: ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目: 来源: 题型:
【题目】某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .估计该校学生每周平均体育运动时间超过6个小时的概率.
.估计该校学生每周平均体育运动时间超过6个小时的概率.
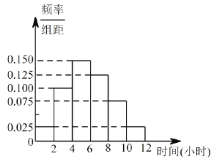
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
|
|
|
|
|
|
|
|
|
|
附: .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)![]() 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求![]() 的分布列与数学期望.
的分布列与数学期望.
(注:若三个数![]() 满足
满足![]() ,则称
,则称![]() 为这三个数的中位数).
为这三个数的中位数).
查看答案和解析>>
科目: 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com