【题目】已知函数，

（1）讨论函数的单调性；

（2）函数有两个极值点，且，求证:.

【题目】已知函数（其中，为自然对数的底数，）.

（1）若，求函数的单调区间；

（2）证明：当时，函数有两个零点，且.

【题目】某市为了增强民众防控病毒的意识，举行了“预防新冠病毒知识竞赛”网上答题，随机抽取人，答题成绩统计如图所示.

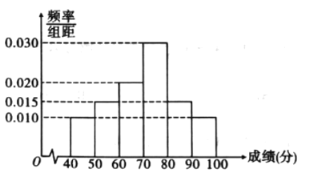
（1）由直方图可认为答题者的成绩服从正态分布，其中，分别为答题者的平均成绩和成绩的方差，那么这名答题者成绩超过分的人数估计有多少人？（同一组中的数据用该组的区间中点值作代表）

（2）如果成绩超过分的民众我们认为是“防御知识合格者”，用这名答题者的成绩来估计全市的民众，现从全市中随机抽取人，“防御知识合格者”的人数为，求.（精确到）

附：①，；②，则，；③，.

【题目】在某企业中随机抽取了5名员工测试他们的艺术爱好指数和创新灵感指数，统计结果如下表（注：指数值越高素质越优秀）：

（1）求创新灵感指数关于艺术爱好指数的线性回归方程；

（2）企业为提高员工的艺术爱好指数，要求员工选择音乐和绘画中的一种进行培训，培训音乐次数对艺术爱好指数的提高量为，培训绘画次数对艺术爱好指数的提高量为，其中为参加培训的某员工已达到的艺术爱好指数.艺术爱好指数已达到3的员工甲选择参加音乐培训，艺术爱好指数已达到4的员工乙选择参加绘画培训，在他们都培训了20次后，估计谁的创新灵感指数更高？

参考公式：回归方程中，，.

参考数据：，

【题目】根据以往的经验，某工程施工期间的降水量（单位：）对工期的影响如下表：

历年气象资料表明，该工程施工期间降水量小于、、的概率分别为、、，求：

（1）在降水量至少是的条件下，工期延误不超过天的概率；

（2）工期延误天数的均值与方差.

方案一：一个不透明的盒子中装有30个质地均匀且大小相同的小球，其中10个红球，20个白球，搅拌均匀后，顾客从中随机抽取一个球，若抽到红球则顾客获得60元的返金券，若抽到白球则获得20元的返金券，且顾客有放回地抽取3次.

方案二：一个不透明的盒子中装有30个质地均匀且大小相同的小球，其中10个红球，20个白球，搅拌均匀后，顾客从中随机抽取一个球，若抽到红球则顾客获得80元的返金券，若抽到白球则未中奖，且顾客有放回地抽取3次.

（1）现有两位顾客均获得抽奖机会，且都按方案一抽奖，试求这两位顾客均获得180元返金券的概率；

（2）若某顾客获得抽奖机会.

①试分别计算他选择两种抽奖方案最终获得返金券的数学期望；

②为了吸引顾客消费，让顾客获得更多金额的返金券，该超市应选择哪一种抽奖方案进行促销活动？

【题目】某中学高三年级在返校复学后，为了做好疫情防护工作，一位防疫督察员要将2盒完全相同的口罩和3盒完全相同的普通医用口罩全部分配给3个不同的班，每个班至少分得一盒，则不同的分法种数是（ ）

A.B.C.D.

附：K2

由此得出的正确结论是（ ）

A.在犯错误的概率不超过0.01的前提下，认为“身高与性别无关”

B.在犯错误的概率不超过0.01的前提下，认为“身高与性别有关”

C.有99.9%的把握认为“身高与性别无关”

D.有99.9%的把握认为“身高与性别有关”

【题目】如图，在多面体中，四边形为矩形，直线与平面所成的角为，，，，.

（1）求证：直线平面；

（2）点在线段上，且，求二面角的余弦值.

A.B.C.D.