
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,
,![]() 是椭圆
是椭圆![]() 上一点.
上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上一点,判断直线
上一点,判断直线![]() 与
与![]() 的斜率之和是否为定值,如果是,请求出此定值,如果不是,请说明理由.
的斜率之和是否为定值,如果是,请求出此定值,如果不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为了鼓励运动提高所有用户的身体素质,特推出一款运动计步数的软件,所有用户都可以通过每天累计的步数瓜分红包,大大增加了用户走步的积极性,所以该软件深受广大用户的欢迎.该公司为了研究“日平均走步数和性别是否有关”,统计了2019年1月份所有用户的日平均步数,规定日平均步数不少于8000的为“运动达人”,步数在8000以下的为“非运动达人”,采用按性别分层抽样的方式抽取了100个用户,得到如下列联表:
运动达人 | 非运动达人 | 总计 | |
男 | 35 | 60 | |
女 | 26 | ||
总计 | 100 |
(1)(i)将![]() 列联表补充完整;
列联表补充完整;
(ii)据此列联表判断,能否有![]() 的把握认为“日平均走步数和性别是否有关”?
的把握认为“日平均走步数和性别是否有关”?
(2)从样本中的运动达人中抽取7人参加“幸运抽奖”活动,通过抽奖共产生2位幸运用户,求这2位幸运用户恰好男用户和女用户各一位的概率.
附:
|
|
|
|
|
|
|
|
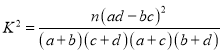
查看答案和解析>>
科目: 来源: 题型:
【题目】下列关于命题的说法错误的是( )
A. 命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B. “![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
C. 命题“![]() ,使得
,使得![]() ”的否定是“
”的否定是“![]() ,均有
,均有![]() ”
”
D. “若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题为真命题
”的逆命题为真命题
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ),在以原点
),在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 有公共点,且直线
有公共点,且直线![]() 与曲线
与曲线![]() 的交点
的交点![]() 恰好在曲线
恰好在曲线![]() 与
与![]() 轴围成的区域(不含边界)内,求
轴围成的区域(不含边界)内,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且原点到直线
,且原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若不经过点![]() 的直线
的直线![]() :
:![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与圆
两点,且与圆![]() 相切.试探究
相切.试探究![]() 的周长是否为定值,若是,求出定值;若不是,请说明理由.
的周长是否为定值,若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x>0时,![]() .
.
(1)求f(x)的解析式;
(2)设x∈[1,2]时,函数![]() ,是否存在实数m使得g(x)的最小值为6,若存在,求m的取值;若不存在,说明理由.
,是否存在实数m使得g(x)的最小值为6,若存在,求m的取值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知甲、乙两名工人在同样条件下每天各生产100件产品,且每生产1件正品可获利20元,生产1件次品损失30元,甲,乙两名工人100天中出现次品件数的情况如表所示.
甲每天生产的次品数/件 | 0 | 1 | 2 | 3 | 4 |
对应的天数/天 | 40 | 20 | 20 | 10 | 10 |
乙每天生产的次品数/件 | 0 | 1 | 2 | 3 |
对应的天数/天 | 30 | 25 | 25 | 20 |
(1)将甲每天生产的次品数记为![]() (单位:件),日利润记为
(单位:件),日利润记为![]() (单位:元),写出
(单位:元),写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)如果将统计的100天中产生次品量的频率作为概率,记![]() 表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量
表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
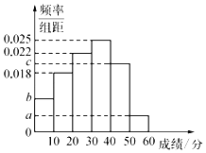
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: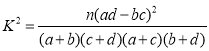 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某次数学测验共有12道选择题,每道题共有四个选项,且其中只有一个选项是正确的,评分标准规定:每选对1道题得5分,不选或选错得0分. 在这次数学测验中,考生甲每道选择题都按照规则作答,并能确定其中有9道题能选对;其余3道题无法确定正确选项,在这3道题中,恰有2道能排除两个错误选项,另1题只能排除一个错误选项. 若考生甲做这3道题时,每道题都从不能排除的选项中随机挑选一个选项作答,且各题作答互不影响.在本次测验中,考生甲选择题所得的分数记为![]()
(1)求![]() 的概率;
的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】法国有个名人叫做布莱尔·帕斯卡,他认识两个赌徒,这两个赌徒向他提出一个问题,他们说,他们下赌金之后,约定谁先赢满5局,谁就获得全部赌金700法郎,赌了半天,甲赢了4局,乙赢了3局,时间很晚了,他们都不想再赌下去了.假设每局两赌徒输赢的概率各占![]() ,每局输赢相互独立,那么这700法郎如何分配比较合理( )
,每局输赢相互独立,那么这700法郎如何分配比较合理( )
A.甲400法郎,乙300法郎B.甲500法郎,乙200法郎
C.甲525法郎,乙175法郎D.甲350法郎,乙350法郎
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com