
科目: 来源: 题型:
【题目】已知函数f(x)=|x+1|.
(1)若不等式f(x)≥|2x+1|1的解集为A,且![]() ,求实数t的取值范围;
,求实数t的取值范围;
(2)在(1)的条件下,若![]() ,证明:f(ab)>f(a)f(b).
,证明:f(ab)>f(a)f(b).
查看答案和解析>>
科目: 来源: 题型:
【题目】全民健身倡导全民做到每天参加一次以上的体育健身活动,旨在全面提高国民体质和健康水平.某市的体育部门对某小区的4000人进行了“运动参与度”统计评分(满分100分),得到了如下的频率分布直方图:
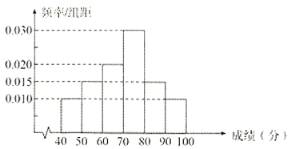
(1)求这4000人的“运动参与度”的平均得分![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由直方图可认为这4000人的“运动参与度”的得分![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() ,
,![]() 分别取平均得分
分别取平均得分![]() 和方差
和方差![]() ,那么选取的4000人中“运动参与度”得分超过84.81分(含84.81分)的人数估计有多少人?
,那么选取的4000人中“运动参与度”得分超过84.81分(含84.81分)的人数估计有多少人?
(3)如果用这4000人得分的情况来估计全市所有人的得分情况,现从全市随机抽取4人,记“运动参与度”的得分不超过84.81分的人数为![]() ,求
,求![]() .(精确到0.001)
.(精确到0.001)
附:①![]() ,
,![]() ;②
;②![]() ,则
,则![]() ,
,![]() ;③
;③![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),以坐标原点为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系,已知曲线C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系,已知曲线C的极坐标方程为![]() ,且直线l经过曲线C的左焦点F.
,且直线l经过曲线C的左焦点F.
(1)求直线l的普通方程;
(2)设曲线C的内接矩形的周长为L,求L的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ln(2+ax)(a>0),![]() (b∈R).
(b∈R).
(1)若函数f(x)的图象在点(3,f(3))处的切线与函数g(x)的图象在点(1,g(1))处的切线平行,求a,b之间的关系;
(2)在(1)的条件下,若b=a,且f(x)≥mg(x)对任意x∈[![]() ,+∞)恒成立,求实数m的取值范围.
,+∞)恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点O为坐标原点,椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,离心率为
(a>b>0)的左、右焦点分别为F1,F2,离心率为![]() ,点I,J分别是椭圆C的右顶点、上顶点,△IOJ的边IJ上的中线长为
,点I,J分别是椭圆C的右顶点、上顶点,△IOJ的边IJ上的中线长为![]() .
.
(1)求椭圆C的标准方程;
(2)过点H(-2,0)的直线交椭圆C于A,B两点,若AF1⊥BF1,求直线AB的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,∠BAC=120°,AC=AB=2,AA1=3.
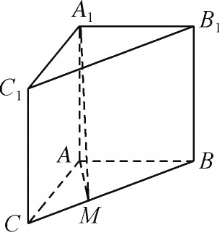
(1)求三棱柱ABC-A1B1C1的体积;
(2)若M是棱BC的一个靠近点C的三等分点,求二面角A-A1M-B的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】费马点是指三角形内到三角形三个顶点距离之和最小的点。当三角形三个内角均小于![]() 时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等均为
时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等均为![]() 。根据以上性质,函数
。根据以上性质,函数![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年双11当天,某购物平台的销售业绩高达2135亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系,现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.9,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为140次.
(1)请完成下表,并判断是否可以在犯错误概率不超过0.5%的前提下,认为商品好评与服务好评有关?
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 140 | ||
对商品不满意 | 10 | ||
合计 | 200 |
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为X.
①求随机变量X的分布列;
②求X的数学期望和方差.
附:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,有一种游戏画板,要求参与者用六种颜色给画板涂色,这六种颜色分别为红色、黄色1、黄色2、黄色3、金色1、金色2,其中黄色1、黄色2、黄色3是三种不同的颜色,金色1、金色2是两种不同的颜色,要求红色不在两端,黄色1、黄色2、黄色3有且仅有两种相邻,则不同的涂色方案有( )

A.120种B.240种C.144种D.288种
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在等比数列{an}中,![]() =2,,
=2,,![]() =128,数列{bn}满足b1=1,b2=2,且{
=128,数列{bn}满足b1=1,b2=2,且{![]() }为等差数列.
}为等差数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com