
科目: 来源: 题型:
【题目】现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是![]() ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是![]() ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用![]() 表示张同学答对题的个数,求
表示张同学答对题的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一次数学竞赛中,某些选手是朋友关系.记所有选手的集合为X,对集合X的子集Y,若可以将这些人两两分组,且每组中两名选手均是朋友关系,则称子集Y“可两两分组”.已知集合X不可两两分组,且对于任意选手![]() ,若A、B不是朋友关系,则
,若A、B不是朋友关系,则![]() 可两两分组,且X中没有一个人与其他所有人均为朋友关系证明:对任意选手
可两两分组,且X中没有一个人与其他所有人均为朋友关系证明:对任意选手![]() ,若a、b为朋友关系,b、c为朋友关系,则a、c也为朋友关系
,若a、b为朋友关系,b、c为朋友关系,则a、c也为朋友关系
查看答案和解析>>
科目: 来源: 题型:
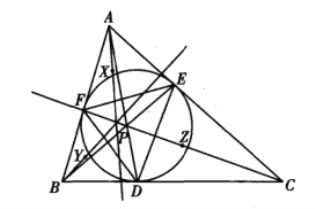
【题目】如图,△ABC的内切圆分别与边BC、CA、AB切于点D、E、F,AD与BE交于点P,设点P关于直线EF、FD、DE的对称点分别X、Y、Z.证明:AX、BY、CZ三线共点.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(Ⅰ)求第一次检测出的是次品且第二次检测出的是正品的概率;
(Ⅱ)已知每检测一件产品需要费用100元,设![]() 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求
表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为直角坐标原点,以极轴为
为直角坐标原点,以极轴为![]() 轴的正半轴建立平面直角坐标系
轴的正半轴建立平面直角坐标系![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度,再将得到的曲线上的每一个点的横坐标缩短为原来的
个单位长度,再将得到的曲线上的每一个点的横坐标缩短为原来的![]() ,纵坐标保持不变,得到曲线
,纵坐标保持不变,得到曲线![]()
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),点
为参数),点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,试问在
,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() 使得直线
使得直线![]() 与直线
与直线![]() 恰关于
恰关于![]() 轴对称?若存在,求出点
轴对称?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com