【题目】已知半径为5的圆的圆心在x轴上，圆心的横坐标是整数，且与直线相切．

（1）求圆的方程；

（2）若直线与圆相交于A，B两点，是否存在实数a，使得过点的直线l垂直平分弦AB？若存在，求出实数a的值；若不存在，请说明理由．

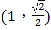【题目】已知椭圆的左、右焦点为别为F1、F2，且过点和．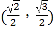

（1）求椭圆的标准方程；

（2）如图，点A为椭圆上一位于x轴上方的动点，AF2的延长线与椭圆交于点B，AO的延长线与椭圆交于点C，求△ABC面积的最大值，并写出取到最大值时直线BC的方程．

【题目】已知抛物线的焦点为，为坐标原点，是抛物线上异于的两点．

（1）求抛物线的方程；

（2）若直线的斜率之积为，求证：直线过定点．

【题目】经济订货批量模型，是目前大多数工厂、企业等最常采用的订货方式，即某种物资在单位时间的需求量为某常数，经过某段时间后，存储量消耗下降到零，此时开始订货并随即到货，然后开始下一个存储周期，该模型适用于整批间隔进货、不允许缺货的存储问题，具体如下：年存储成本费（元）关于每次订货（单位）的函数关系，其中为年需求量，为每单位物资的年存储费，为每次订货费. 某化工厂需用甲醇作为原料，年需求量为6000吨，每吨存储费为120元/年，每次订货费为2500元.

（1）若该化工厂每次订购300吨甲醇，求年存储成本费；

（2）每次需订购多少吨甲醇，可使该化工厂年存储成本费最少？最少费用为多少？

【题目】已知四棱锥的底面为直角梯形，，°，底面，且，是的中点.

（1）证明：平面平面；

（2）求与所成角的余弦值；

（3）求平面与平面所成二面角（锐角）的余弦值.

【题目】如图，在四棱锥中，底面是梯形，且，，点是线段的中点，过的平面交平面于，且，，且，，.

（1）求证：；

（2）求直线与平面所成角的余弦值.

【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面底面ABCD,且,若E,F分别为PC,BD的中点.

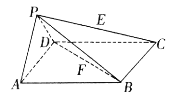
(I)求证:EF//平面PAD;

(II)求三棱锥F-DEC的体积;

(III)在线段CD上是否存在一点G,使得平面平面PDC?若存在,请说明其位置,并加以证明;若不存在,请说明理由.

（1）在所有参与调查的人中，用分层抽样的方法抽取n个人，已知从“支持A方案”的人中抽取了6人，求n的值；

（2）在“支持B方案”的人中，用分层抽样的方法抽取5人看作一个总体，从这5人中任意选取2人，求恰好有1人在35岁以上（含35岁）的概率.

（1）求证：EF∥平面PAB；

（2）若PB与平面ABCD所成角的正弦值为，求二面角P-AE-B的余弦值．

（1）求证：AF∥平面PEC

（2）求证：平面PCD⊥平面PEC；

（3）求三棱锥C-BEP的体积．