
科目: 来源: 题型:
【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年11月5日至10日,首届中国国际进口博览会在国家会展中心(上海)举行,吸引过来58个“一带一路”沿线国家的超过1000多家企业参展,成为共建“一带一路”的又一个重要支撑。某企业为了参加这次盛会,提升行业竞争力,加大了科技投入;该企业连续6年来得科技投入![]() (百万元)与收益
(百万元)与收益![]() (百万元)的数据统计如下:
(百万元)的数据统计如下:

根据散点图的特点,甲认为样本点分布在指数曲线![]() 的周围,据此他对数据进行了一些初步处理,如下表:
的周围,据此他对数据进行了一些初步处理,如下表:

其中![]() ,
,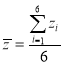 .
.
(1)(![]() )请根据表中数据,建立
)请根据表中数据,建立![]() 关于
关于![]() 的回归方程(保留一位小数);
的回归方程(保留一位小数);
(![]() )根据所建立回归方程,若该企业想在下一年的收益达到2亿,则科技投入的费用至少要多少(其中
)根据所建立回归方程,若该企业想在下一年的收益达到2亿,则科技投入的费用至少要多少(其中![]() )?
)?
(2)乙认为样本点分布在二次曲线![]() 的周围,并计算得回归方程为
的周围,并计算得回归方程为![]() ,以及该回归模型的相关指数
,以及该回归模型的相关指数![]() ,试比较甲乙两位员工所建立的模型,谁的拟合效果更好.
,试比较甲乙两位员工所建立的模型,谁的拟合效果更好.
附:对于一组数据![]() ,
,![]() ,……
,……![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为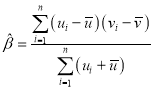 ,
,![]() ,相关指数:
,相关指数: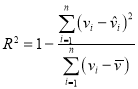 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,过左焦点的直线
,过左焦点的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点(异于
两点(异于![]() 、
、![]() 两点),当直线
两点),当直线![]() 垂直于
垂直于![]() 轴时,四边形
轴时,四边形![]() 的面积为6.
的面积为6.
(1)求椭圆的方程;
(2)设直线![]() 、
、![]() 的交点为
的交点为![]() ;试问
;试问![]() 的横坐标是否为定值?若是,求出定值;若不是,请说明理由.
的横坐标是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】十九大提出,坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮助贫困村种植蜜柚,并利用电商进行销售,为了更好地销售,现从该村的蜜柚树上随机摘下了![]() 个蜜柚进行测重,其质量分别在
个蜜柚进行测重,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() (单位:克)中,其频率分布直方图如图所示,
(单位:克)中,其频率分布直方图如图所示,

(Ⅰ)已经按分层抽样的方法从质量落在![]() ,
,![]() 的蜜柚中抽取了
的蜜柚中抽取了![]() 个,现从这
个,现从这![]() 个蜜柚中随机抽取
个蜜柚中随机抽取![]() 个。求这
个。求这![]() 个蜜柚质量均小于
个蜜柚质量均小于![]() 克的概率:
克的概率:
(Ⅱ)以各组数据的中间值代表这组数据的平均水平,以频率代表概率,已知该贫困村的蜜柚树上大约还有![]() 个蜜柚等待出售,某电商提出了两种收购方案:
个蜜柚等待出售,某电商提出了两种收购方案:
方案一:所有蜜柚均以![]() 元/千克收购;
元/千克收购;
方案二:低于![]() 克的蜜柚以
克的蜜柚以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
请你通过计算为该村选择收益最好的方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求函数![]() 的单调区间;
的单调区间;
(Ⅲ)用![]() 表示
表示![]() ,
,![]() 中的较大者,记函数
中的较大者,记函数![]() .若函数
.若函数![]() 在
在![]() 内恰有2个零点,求实数
内恰有2个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且短轴长为
,且短轴长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,设点
,设点![]() 为第四象限内一点且在椭圆
为第四象限内一点且在椭圆![]() 上(点
上(点![]() 不在直线
不在直线![]() 上),点
上),点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于另一点
交于另一点![]() .设
.设![]() 为坐标原点,判断直线
为坐标原点,判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知动圆![]() 与
与![]() 轴相切,且与圆
轴相切,且与圆![]() :
:![]() 外切;
外切;
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若直线![]() 过定点
过定点![]() ,且与轨迹
,且与轨迹![]() 交于
交于![]() 、
、![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 、
、![]() 两点,若点
两点,若点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求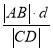 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com