
科目: 来源: 题型:
【题目】2021年福建省高考实行“![]() ”模式.“
”模式.“![]() ”模式是指:“3”为全国统考科目语文、数学、外语,所有学生必考;“1”为首选科目,考生须在高中学业水平考试的物理、历史科目中选择1科;“2”为再选科目,考生可在化学、生物、政治、地理4个科目中选择2科,共计6个考试科目.
”模式是指:“3”为全国统考科目语文、数学、外语,所有学生必考;“1”为首选科目,考生须在高中学业水平考试的物理、历史科目中选择1科;“2”为再选科目,考生可在化学、生物、政治、地理4个科目中选择2科,共计6个考试科目.
(1)若学生甲在“1”中选物理,在“2”中任选2科,求学生甲选化学和生物的概率;
(2)若学生乙在“1”中任选1科,在“2”中任选2科,求学生乙不选政治但选生物的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】将函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() 倍(纵坐标不变)得到函数
倍(纵坐标不变)得到函数![]() 的图像,则下列说法正确的是( )
的图像,则下列说法正确的是( )
A. 函数![]() 的最小正周期为
的最小正周期为![]()
B. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
C. 函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]()
D. ![]() 是函数
是函数![]() 的一条对称轴
的一条对称轴
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市在进行创建文明城市的活动中,为了解居民对“创文”的满意程度,组织居民给活动打分(分数为整数.满分为100分).从中随机抽取一个容量为120的样本.发现所有数据均在![]() 内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:
内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:
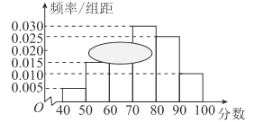
(1)算出第三组![]() 的频数.并补全频率分布直方图;
的频数.并补全频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数、中位数和平均数.(每组数据以区间的中点值为代表)
查看答案和解析>>
科目: 来源: 题型:
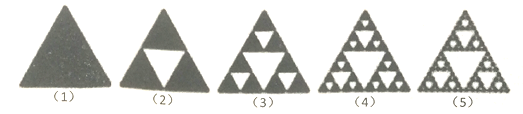
【题目】谢尔宾斯基三角形(Sierpinski triangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出.在一个正三角形中,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,我们用白色三角形代表挖去的部分,黑色三角形为剩下的部分,我们称此三角形为谢尔宾斯基三角形.若在图(3)内随机取一点,则此点取自谢尔宾斯基三角形的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知动圆与圆![]() 相切,且与圆
相切,且与圆![]() 相内切,记圆心的轨迹为曲线.
相内切,记圆心的轨迹为曲线.
(Ⅰ)求曲线C的方程;
(Ⅱ)设Q为曲线C上的一个不在轴上的动点,O为坐标原点,过点![]() 作OQ的平行线交曲线C于M,N两个不同的点, 求△QMN面积的最大值.
作OQ的平行线交曲线C于M,N两个不同的点, 求△QMN面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 经过点
经过点![]() ,且点
,且点![]() 为其一个焦点.
为其一个焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 与
与![]() 轴的两个交点为
轴的两个交点为![]() ,
,![]() ,不在
,不在![]() 轴上的动点
轴上的动点![]() 在直线
在直线![]() 上运动,直线
上运动,直线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于点
交于点![]() ,
,![]() ,证明:直线
,证明:直线![]() 通过一个定点,且
通过一个定点,且![]() 的周长为定值.
的周长为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com