
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() 有两个相异零点
有两个相异零点![]() ,求证:
,求证:![]() .
.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)对f′(x)![]() 中的k分类讨论,根据f′(x)的正负判断函数
中的k分类讨论,根据f′(x)的正负判断函数![]() 的单调性即可.
的单调性即可.
(2)由题意得lnx1﹣kx1=0,lnx2﹣kx2=0,两式作差可得,lnx1﹣lnx2=k(x1﹣x2),k=![]() ,要证lnx1+lnx2>2即k(x1+x2)>2,将k代换后,化简变形得
,要证lnx1+lnx2>2即k(x1+x2)>2,将k代换后,化简变形得![]() ,设t
,设t![]() 1,构造函数g(t),利用新函数的导数求出单调区间,证得g(t)>g(1)=0即可.
1,构造函数g(t),利用新函数的导数求出单调区间,证得g(t)>g(1)=0即可.
(1)![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递增;
上单调递增;
②当![]() 时,由
时,由![]() ,得
,得![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
(2)因为![]() ,
,![]() 是
是![]() 的两个零点,则
的两个零点,则![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
要证![]() ,只要证
,只要证![]() ,即证
,即证![]() ,
,
即证![]() ,即证
,即证![]() ,只要证
,只要证![]() .
.
设![]() ,则只要证
,则只要证![]() .
.
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为原点,其焦点
的顶点为原点,其焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .设
.设![]() 为直线
为直线![]() 上的点,过点
上的点,过点![]() 作抛物线
作抛物线![]() 的两条切线
的两条切线![]() ,其中
,其中![]() 为切点.
为切点.
(1) 求抛物线![]() 的方程;
的方程;
(2) 当点![]() 为直线
为直线![]() 上的定点时,求直线
上的定点时,求直线![]() 的方程;
的方程;
(3) 当点![]() 在直线
在直线![]() 上移动时,求
上移动时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x2+1)﹣e﹣|x|(e为自然对数的底数),则不等式f(2x+1)>f(x)的解集是( )
A. (﹣1,1)B. (﹣∞,﹣1)∪(1,+∞)
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在同一直角坐标系中,经过伸缩变换 后,曲线C的方程变为
后,曲线C的方程变为![]() .以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线/的极坐标方程为
.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线/的极坐标方程为![]() .
.
(1)求曲线C和直线l的直角坐标方程;
(2)过点![]() 作l的垂线l0交C于A,B两点,点A在x轴上方,求
作l的垂线l0交C于A,B两点,点A在x轴上方,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进![]() 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝,![]() )的函数解析式.
)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
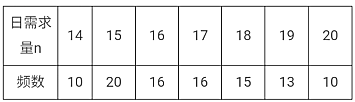
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进![]() 枝玫瑰花,
枝玫瑰花,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列,数学期望及方差;
的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年福建省高考实行“![]() ”模式.“
”模式.“![]() ”模式是指:“3”为全国统考科目语文、数学、外语,所有学生必考;“1”为首选科目,考生须在高中学业水平考试的物理、历史科目中选择1科;“2”为再选科目,考生可在化学、生物、政治、地理4个科目中选择2科,共计6个考试科目.
”模式是指:“3”为全国统考科目语文、数学、外语,所有学生必考;“1”为首选科目,考生须在高中学业水平考试的物理、历史科目中选择1科;“2”为再选科目,考生可在化学、生物、政治、地理4个科目中选择2科,共计6个考试科目.
(1)若学生甲在“1”中选物理,在“2”中任选2科,求学生甲选化学和生物的概率;
(2)若学生乙在“1”中任选1科,在“2”中任选2科,求学生乙不选政治但选生物的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的定义域为
的定义域为![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,关于
成立,关于![]() 的不等式
的不等式![]() 的解集记为
的解集记为![]() .
.
(1)若![]() 为真,求实数
为真,求实数![]() 的取值集合
的取值集合![]() ;
;
(2)在(1)的条件下,若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点为
的左、右顶点为![]() ,
,![]() ,椭圆上任意一点
,椭圆上任意一点![]() ,满足
,满足![]() ,且椭圆过点
,且椭圆过点![]() .
.
(1)求椭圆的标准方程;
(2)设![]() 是轨迹
是轨迹![]() 上的两个动点,线段
上的两个动点,线段![]() 的中点
的中点![]() 在直线
在直线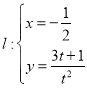 (为参数)上,线段
(为参数)上,线段![]() 的中垂线与
的中垂线与![]() 交于
交于![]() 两点,是否存在点
两点,是否存在点![]() ,使以
,使以![]() 为直径的圆经过点
为直径的圆经过点![]() ,若存在,求出
,若存在,求出![]() 点坐标,若不存在,请说明理由.
点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A.命题“若![]() ⊥
⊥![]() ,则
,则![]()
![]() 0”的否命题为“若
0”的否命题为“若![]() ⊥
⊥![]() ,则
,则![]()
![]() 0”
0”
B.命题“函数f(x)=(a﹣1)x是R上的增函数”的否定是“函数f(x)=(a﹣1)x是R上的减函数”
C.命题“在△ABC中,若sinA=sinB,则A=B”的逆否命题为真命题
D.命题“若x=2,则x2﹣3x+2=0”的逆命题为真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com