
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l:x![]() y
y![]() 2=0,抛物线C:y2=2px(p>0).
2=0,抛物线C:y2=2px(p>0).

(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证:线段PQ的中点坐标为![]() ;
;
②求p的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长为
为边长为![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥
的正方形,△ABE和△BCF均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 在棱
在棱![]() 上,满足
上,满足![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() 的左、右焦点,椭圆
的左、右焦点,椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() (不过坐标原点)与椭圆
(不过坐标原点)与椭圆![]() 交于
交于![]() ,
,![]() 两点,且点
两点,且点![]() 在
在![]() 轴上方,点
轴上方,点![]() 在
在![]() 轴下方,若
轴下方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数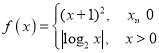 ,若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则
,若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则![]() 的取值范围为( )
的取值范围为( )
A. (﹣1,+∞)B. (﹣1,1]C. (﹣∞,1)D. [﹣1,1)
查看答案和解析>>
科目: 来源: 题型:
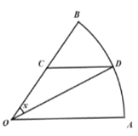
【题目】为庆祝某校一百周年校庆,展示该校一百年来的办学成果及优秀校友风采,学校准备校庆期间搭建一个扇形展览区,如图,是一个半径为2百米,圆心角为![]() 的扇形展示区的平面示意图.点
的扇形展示区的平面示意图.点![]() 是半径
是半径![]() 上一点,点
上一点,点![]() 是圆弧
是圆弧![]() 上一点,且
上一点,且![]() .为了实现“以展养展”,现决定:在线段
.为了实现“以展养展”,现决定:在线段![]() 、线段
、线段![]() 及圆弧
及圆弧![]() 三段所示位置设立广告位,经测算广告位出租收入是:线段
三段所示位置设立广告位,经测算广告位出租收入是:线段![]() 处每百米为
处每百米为![]() 元,线段
元,线段![]() 及圆弧
及圆弧![]() 处每百米均为
处每百米均为![]() 元.设
元.设![]() 弧度,广告位出租的总收入为
弧度,广告位出租的总收入为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)试问![]() 为何值时,广告位出租的总收入最大,并求出其最大值.
为何值时,广告位出租的总收入最大,并求出其最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与x轴平行,求a的值;
处的切线与x轴平行,求a的值;
(Ⅱ)若![]() 在
在![]() 处取得极大值,求a的取值范围;
处取得极大值,求a的取值范围;
(Ⅲ)当a=2时,若函数![]() 有3个零点,求m的取值范围.(只需写出结论)
有3个零点,求m的取值范围.(只需写出结论)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,经过点B(0,1).设椭圆G的右顶点为A,过原点O的直线l与椭圆G交于P,Q两点(点Q在第一象限),且与线段AB交于点M.
,经过点B(0,1).设椭圆G的右顶点为A,过原点O的直线l与椭圆G交于P,Q两点(点Q在第一象限),且与线段AB交于点M.
(Ⅰ)求椭圆G的标准方程;
(Ⅱ)是否存在直线l,使得△BOP的面积是△BMQ的面积的3倍?若存在,求直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,AB=2,BC=1,![]() ,E为PB中点.
,E为PB中点.
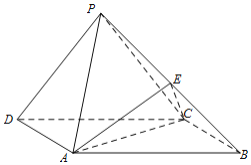
(Ⅰ)求证:PD∥平面ACE;
(Ⅱ)求证:PD⊥平面PBC;
(Ⅲ)求三棱锥E-ABC的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,设M,N是椭圆C上位于x轴上方的两动点,且直线
,设M,N是椭圆C上位于x轴上方的两动点,且直线![]() 与直线
与直线![]() 平行,
平行,![]() 与
与![]() 交于点D.
交于点D.
(Ⅰ)求![]() 和
和![]() 的坐标;
的坐标;
(Ⅱ)求![]() 的最小值;
的最小值;
(Ⅲ)求证:![]() 是定值.
是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com