
科目: 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的焦距等于短轴的长,椭圆的右顶点到左焦点
)的焦距等于短轴的长,椭圆的右顶点到左焦点![]() 的距离为
的距离为![]() .
.
(1)求椭圆C的标准方程;
(2)已知直线l:![]() (
(![]() )与椭圆C交于A、B两点,在y轴上是否存在点
)与椭圆C交于A、B两点,在y轴上是否存在点![]() ,使得
,使得![]() ,且
,且![]() ,若存在,求实数t的取值范围;若不存在,请说明理由.
,若存在,求实数t的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂要建造一个长方体无盖贮水池,其容积为![]() ,深3m.如果池底每平方米的造价为200元,池壁每平方米的造价为150元,怎样设计水池能使总造价最低?最低总造价是多少?
,深3m.如果池底每平方米的造价为200元,池壁每平方米的造价为150元,怎样设计水池能使总造价最低?最低总造价是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]()
![]() 两焦点,若存在直线
两焦点,若存在直线![]() ,使得
,使得![]() ,
,![]() 关于
关于![]() 的对称点的连线恰好是圆
的对称点的连线恰好是圆![]()
![]() 的一条直径.
的一条直径.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的上顶点
的上顶点![]() 作斜率为
作斜率为![]() ,
,![]() 的两条直线
的两条直线![]() ,
,![]() ,两直线分别与椭圆交于
,两直线分别与椭圆交于![]() ,
,![]() 两点,当
两点,当![]() 时,直线
时,直线![]() 是否过定点?若是求出该定点,若不是请说明理由.
是否过定点?若是求出该定点,若不是请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图甲是某商店2018年(按360天计算)的日盈利额(单位:万元)的统计图.
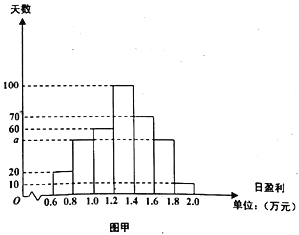
(1)请计算出该商店2018年日盈利额的平均值(精确到0.1,单位:万元):
(2)为了刺激消费者,该商店于2019年1月举行有奖促销活动,顾客凡购买一定金额的高品后均可参加抽奖.随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该商店对前5天抽奖活动的人数进行统计如下表:(![]() 表示第
表示第![]() 天参加抽奖活动的人数)
天参加抽奖活动的人数)
| 1 | 2 | 3 | 4 | 5 |
| 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(ⅰ)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() :
:
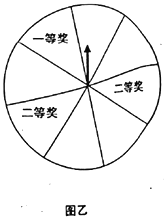
(ⅱ)该商店采取转盘方式进行抽奖(如图乙),其中转盘是个八等分的圆.每位顾客最多两次抽奖机会,若第一次抽到奖,则抽奖终止,若第一次未抽到奖,则再提供一次抽奖机会.抽到一等奖的奖品价值128元,抽到二等奖的奖品价值32元.若该商店此次抽奖活动持续7天,试估计该商店在此次抽奖活动结束时共送出价值为多少元的奖品(精确到0.1,单位:万元)?
(3)用(1)中的2018年日盈利额的平均值去估计当月(共31天)每天的日盈利额.若商店每天的固定支出约为1000元,促销活动日的日盈利额比平常增加20%,则该商店当月的纯利润约为多少万元?(精确到0.1,纯利润=盈利额-固定支出-抽奖总奖金数)
参考公式及数据: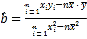 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
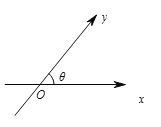
【题目】如图,数轴![]() ,
,![]() 的交点为
的交点为![]() ,夹角为
,夹角为![]() ,与
,与![]() 轴、
轴、![]() 轴正向同向的单位向量分别是
轴正向同向的单位向量分别是![]() ,
,![]() .由平面向量基本定理,对于平面内的任一向量
.由平面向量基本定理,对于平面内的任一向量![]() ,存在唯一的有序实数对
,存在唯一的有序实数对![]() ,使得
,使得![]() ,我们把
,我们把![]() 叫做点
叫做点![]() 在斜坐标系
在斜坐标系![]() 中的坐标(以下各点的坐标都指在斜坐标系
中的坐标(以下各点的坐标都指在斜坐标系![]() 中的坐标).
中的坐标).
(1)若![]() ,
,![]() 为单位向量,且
为单位向量,且![]() 与
与![]() 的夹角为
的夹角为![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若![]() ,点
,点![]() 的坐标为
的坐标为![]() ,求向量
,求向量![]() 与
与![]() 的夹角;
的夹角;
(3)若![]() ,求过点
,求过点![]() 的直线
的直线![]() 的方程,使得原点
的方程,使得原点![]() 到直线
到直线![]() 的距离最大.
的距离最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() ,设直线
,设直线![]() ,其中
,其中![]() ,给出下列结论:
,给出下列结论:
①直线![]() 的方向向量与向量
的方向向量与向量![]() 共线;
共线;
②若![]() ,则直线
,则直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ;
;
③直线![]() 与直线
与直线![]() (
(![]() )一定平行;
)一定平行;
写出所有真命题的序号________
查看答案和解析>>
科目: 来源: 题型:
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]:在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (t为参数,
(t为参数,![]() ),以坐标原点为极点,以x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为
),以坐标原点为极点,以x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() ,已知直线
,已知直线![]() 与曲线C交于不同的两点A,B.
与曲线C交于不同的两点A,B.
(1)求直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)设P(1,2),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com