
科目: 来源: 题型:
【题目】已知双曲线![]() :
:![]() 经过点
经过点![]() ,且其中一焦点
,且其中一焦点![]() 到一条渐近线的距离为1.
到一条渐近线的距离为1.
(1)求双曲线![]() 的方程;
的方程;
(2)过点![]() 作两条相互垂直的直线
作两条相互垂直的直线![]() ,
,![]() 分别交双曲线
分别交双曲线![]() 于
于![]() ,
,![]() 两点,求点
两点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() :
:![]()
![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与抛物线
,与抛物线![]() 的交点为
的交点为![]() ,且
,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过抛物线![]() 上一点
上一点![]() 作两条互相垂直的弦
作两条互相垂直的弦![]() 和
和![]() ,试问直线
,试问直线![]() 是否过定点,若是,求出该定点;若不是,请说明理由.
是否过定点,若是,求出该定点;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某中学学生对数学学习的情况,从该校抽了![]() 名学生,分析了这
名学生,分析了这![]() 名学生某次数学考试成绩(单位:分),得到了如下的频率分布直方图:
名学生某次数学考试成绩(单位:分),得到了如下的频率分布直方图:

(1)求频率分布直方图中![]() 的值;
的值;
(2)根据频率分布直方图估计该组数据的中位数(精确到![]() );
);
(3)在这![]() 名学生的数学成绩中,从成绩在
名学生的数学成绩中,从成绩在![]() 的学生中任选
的学生中任选![]() 人,求次
人,求次![]() 人的成绩都在
人的成绩都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
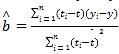 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 均在第一象限),
均在第一象限),![]() 为坐标原点.
为坐标原点.
①证明:直线![]() 的斜率依次成等比数列.
的斜率依次成等比数列.
②若![]() 与
与![]() 关于
关于![]() 轴对称,证明:
轴对称,证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 合计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
合计 | 60 | 50 | 110 |
由K2=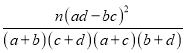 ,
,
附表:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com