
科目: 来源: 题型:
【题目】已知函数f(x)![]() ,x∈R.
,x∈R.
(1)若f(x)是偶函数,求实数a的值;
(2)当a>0时,不等式f(sinx![]() cosx)﹣f(4+t)≥0对任意的x∈
cosx)﹣f(4+t)≥0对任意的x∈![]() 恒成立,求实数t的取值范围;
恒成立,求实数t的取值范围;
(3)当a>0时,关于x的方程![]() 在区间[1,2]上恰有两个不同的实数解,求实数a的取值范围.
在区间[1,2]上恰有两个不同的实数解,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是梯形,
是梯形,![]() ∥
∥![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() .
.
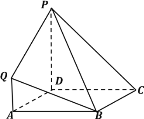
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)已知点![]() 在棱
在棱![]() 上,且异面直线
上,且异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四校锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,边长为4的正△PAD所在平面与平面ABCD垂直,点E是AD的中点,点Q是侧棱PC的中点.

(1)求四棱锥P﹣ABCD的体积;
(2)求证:PA∥平面BDQ;
(3)在线段AB上是否存在点F,使直线PF与平面PAD所成的角为30°?若存在,求出AF的长,若不存在,请说明理由?
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学的甲、乙、丙三名同学参加高校自主招生考试,每位同学彼此独立的从![]() 四所高校中选2所.
四所高校中选2所.
(Ⅰ)求甲、乙、丙三名同学都选![]() 高校的概率;
高校的概率;
(Ⅱ)若已知甲同学特别喜欢![]() 高校,他必选
高校,他必选![]() 校,另在
校,另在![]() 三校中再随机选1所;而同学乙和丙对四所高校没有偏爱,因此他们每人在四所高校中随机选2所.
三校中再随机选1所;而同学乙和丙对四所高校没有偏爱,因此他们每人在四所高校中随机选2所.
(ⅰ)求甲同学选![]() 高校且乙、丙都未选
高校且乙、丙都未选![]() 高校的概率;
高校的概率;
(ⅱ)记![]() 为甲、乙、丙三名同学中选
为甲、乙、丙三名同学中选![]() 校的人数,求随机变量
校的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆![]() 的离心率
的离心率![]() ,抛物线
,抛物线![]() 的焦点恰好是椭圆
的焦点恰好是椭圆![]() 的右焦点
的右焦点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作两条斜率都存在的直线
作两条斜率都存在的直线![]() ,设
,设![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,若
两点,若![]() 是
是![]() 与
与![]() 的等比中项,求
的等比中项,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知bcos(A![]() )
)![]() asin(B
asin(B![]() )=0,且sinA,sinB,2sinC成等比数列.
)=0,且sinA,sinB,2sinC成等比数列.
(1)求角B;
(2)若a+c=λb(λ∈R),求λ的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图l,在边长为2的菱形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.
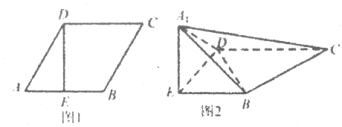
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】茎叶图记录了甲,乙两组各四名同学单位时间内引体向上的次数,乙组记录中有一个数据模糊,无法确认,在图中以X表示.
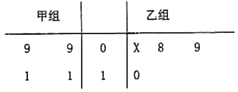
(1)如果X=8,求乙组同学单位时间内引体向上次数的平均数和方差;
(2)如果X=9,分别从甲,乙两组中随机选取一名同学,求这两名同学单位时间内引体向上次数和为19的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了研究学生的数学核素养与抽象(能力指标![]() )、推理(能力指标
)、推理(能力指标![]() )、建模(能力指标
)、建模(能力指标![]() )的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养;若
的值评定学生的数学核心素养;若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
学生编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在这10名学生中任取两人,求这两人的建模能力指标相同的概率;
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为![]() ,从数学核心素养等级不是一级的学生中任取一人,其综合指标为
,从数学核心素养等级不是一级的学生中任取一人,其综合指标为![]() ,记随机变量
,记随机变量![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】设f(x)=asin2x+bcos2x(a,b∈R,ab≠0),若f(x)![]() 对一切x∈R恒成立,给出以下结论:
对一切x∈R恒成立,给出以下结论:
①![]() ;
;
②![]() ;
;
③f(x)的单调递增区间是![]() ;
;
④函数y=f(x)既不是奇函数也不是偶函数;
⑤存在经过点(a,b)的直线与函数f(x)的图象不相交,其中正确结论为_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com