
科目: 来源: 题型:
【题目】每年暑期都会有大量中学生参加名校游学,夏令营等活动,某中学学生社团将其今年的社会实践主题定为“中学生暑期游学支出分析”,并在该市各个中学随机抽取了共![]() 名中学生进行问卷调查,根据问卷调查发现共
名中学生进行问卷调查,根据问卷调查发现共![]() 名中学生参与了各类游学、夏令营等活动,从中统计得到中学生暑期游学支出(单位:百元)频率分布方图如图.
名中学生参与了各类游学、夏令营等活动,从中统计得到中学生暑期游学支出(单位:百元)频率分布方图如图.
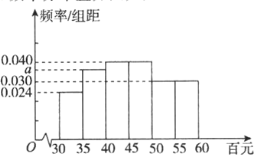
(I)求实数![]() 的值;
的值;
(Ⅱ)在![]() ,
,![]() ,
,![]() 三组中利用分层抽样抽取
三组中利用分层抽样抽取![]() 人,并从抽取的
人,并从抽取的![]() 人中随机选出
人中随机选出![]() 人,对其消费情况进行进一步分析.
人,对其消费情况进行进一步分析.
(i)求每组恰好各被选出![]() 人的概率;
人的概率;
(ii)设![]() 为选出的
为选出的![]() 人中
人中![]() 这一组的人数,求随机变量
这一组的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在R上的函数f(x)满足f(x+2)=f(x),且当x∈[-1,1]时,f(x)=x2.令g(x)=f(x)-kx-k,若在区间[-1,3]内,函数g(x)=0有4个不相等实根,则实数k的取值范围是( )
A.(0,+∞)B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为![]() .现有甲、乙两人从袋中轮流、不放回地摸取1球,甲先取,乙后取,然后甲再取……直到袋中的球取完即终止.若摸出白球,则记2分,若摸出黑球,则记1分.每个球在每一次被取出的机会是等可能的.
.现有甲、乙两人从袋中轮流、不放回地摸取1球,甲先取,乙后取,然后甲再取……直到袋中的球取完即终止.若摸出白球,则记2分,若摸出黑球,则记1分.每个球在每一次被取出的机会是等可能的.
(1)求袋中白球的个数;
(2)用表示甲,乙最终得分差的绝对值,求随机变量![]() 的概率分布列及数学期望E
的概率分布列及数学期望E![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个口袋中有3个红球4个白球,从中取出2个球.下面几个命题:
(1)如果是不放回地抽取,那么取出1个红球,1个白球的概率是![]()
(2)如果是不放回地抽取,那么在至少取出一个红球的条件下,第2次取出红球的概率是![]()
(3)如果是有放回地抽取,那么取出1个红球1个白球的概率是![]()
(4)如果是有放回地抽取,那么第2次取到红球的概率和第1次取到红球的概率相同.
其中正确的命题是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上![]() 件产品作为样本算出他们的重量(单位:克)重量的分组区间为
件产品作为样本算出他们的重量(单位:克)重量的分组区间为![]() ,
,![]() ,……
,……![]() ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.
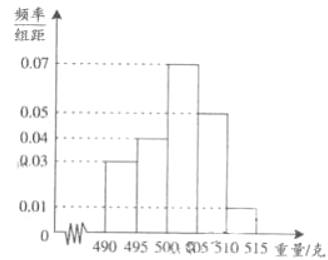
(1)根据频率分布直方图,求重量超过![]() 克的产品数量.
克的产品数量.
(2)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为重量超过
为重量超过![]() 克的产品数量,求
克的产品数量,求![]() 的分布列.
的分布列.
(3)从流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品合格的重量超过
件产品合格的重量超过![]() 克的概率.
克的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xoy中,已知曲线C1:x2+y2=1,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() :ρ(2cosθ-sinθ)=6.
:ρ(2cosθ-sinθ)=6.
(Ⅰ)将曲线C1上的所有点的横坐标,纵坐标分别伸长为原来的![]() 、2倍后得到曲线C2,试写出直线
、2倍后得到曲线C2,试写出直线![]() 的直角坐标方程和曲线C2的参数方程.
的直角坐标方程和曲线C2的参数方程.
(Ⅱ)在曲线C2上求一点P,使点P到直线l的距离最大,并求出此最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】由0,1,2,3,4,5,6,7,8,9组成没有重复数字的五位数,且是奇数,其中恰有两个数字是偶数,则这样的五位数的个数为( ).
A.7200B.6480C.4320D.5040
查看答案和解析>>
科目: 来源: 题型:
【题目】齐王有上等,中等,下等马各一匹;田忌也有上等,中等,下等马各一匹.田忌的上等马优于齐王的中等马,劣于齐王的上等马;田忌的中等马优于齐王的下等马,劣于齐王的中等马;田忌的下等马劣于齐王的下等马.现从双方的马匹中随机各选一匹进行一场比赛,若有优势的马一定获胜,则齐王的马获胜的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米.
(Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com