
科目: 来源: 题型:
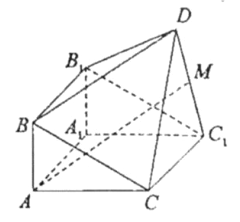
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中,![]() ,平面
,平面![]() 平面
平面![]()
(I)求证:![]() ;
;
(II)若M为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(III)在线段BC上(含端点)是否存在点P,使直线DP与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 得值,若不存在,说明理由.
得值,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知M,N分别为线段BB1,A1C的中点,MN⊥AA1,且MA1=MC.求证:
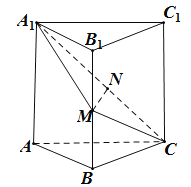
(1)MN![]() 平面ABC;
平面ABC;
(2)平面A1MC⊥平面A1ACC1.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,合肥一中积极开展美丽校园建设,现拟在边长为0.6千米的正方形地块![]() 上划出一片三角形地块
上划出一片三角形地块![]() 建设小型生态园,点
建设小型生态园,点![]() 分别在边
分别在边![]() 上.
上.
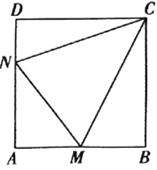
(1)当点![]() 分别时边
分别时边![]() 中点和
中点和![]() 靠近
靠近![]() 的三等分点时,求
的三等分点时,求![]() 的余弦值;
的余弦值;
(2)实地勘察后发现,由于地形等原因,![]() 的周长必须为1.2千米,请研究
的周长必须为1.2千米,请研究![]() 是否为定值,若是,求此定值,若不是,请说明理由.
是否为定值,若是,求此定值,若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A(﹣2,1),B(2,4),点P是直线l:y=x上的动点.
(1)若PA⊥PB,求点P的坐标;
(2)设过A的直线l1与过B的直线l2均平行于l,求l1与l2之间的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l过点A(0,5)且与曲线x2+y2=5(x>0)相切于点B,则直线l的方程是_____,设E是线段OB中点,长度为![]() 的线段PQ(P在Q的上方)在直线l上滑动,则|OP|+|EQ|的最小值是_____.
的线段PQ(P在Q的上方)在直线l上滑动,则|OP|+|EQ|的最小值是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】假设某种设备使用的年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有以下统计资料:
(万元)有以下统计资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系.试求:
呈线性相关关系.试求:
(1)求![]() ;
;
(2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算![]() 的值时,可根据以下公式:
的值时,可根据以下公式: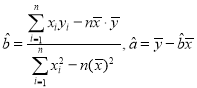
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角△ABC中,AC=![]() ,BC=1,点D是斜边AB上的动点,将△BCD沿着CD翻折至△B'CD,使得点B'在平面ACD内的射影H恰好落在线段CD上,则翻折后|AB'|的最小值是_____.
,BC=1,点D是斜边AB上的动点,将△BCD沿着CD翻折至△B'CD,使得点B'在平面ACD内的射影H恰好落在线段CD上,则翻折后|AB'|的最小值是_____.
查看答案和解析>>
科目: 来源: 题型:
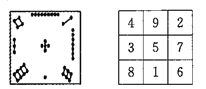
【题目】我国古代的《洛书》中记载着世界上最古老的一个幻方:如图,将1,2,…,9填入![]() 的方格内,使三行,三列和两条对角线上的三个数字之和都等于15.一般地,将连续的正整数
的方格内,使三行,三列和两条对角线上的三个数字之和都等于15.一般地,将连续的正整数![]() 填入
填入![]() 个方格中,使得每行,每列和两条对角线上的数字之和都相等,这个正方形叫做
个方格中,使得每行,每列和两条对角线上的数字之和都相等,这个正方形叫做![]() 阶幻方.记
阶幻方.记![]() 阶幻方的对角线上的数字之和为
阶幻方的对角线上的数字之和为![]() ,如图三阶幻方的
,如图三阶幻方的![]() ,那么
,那么![]() 的值为__________ .
的值为__________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com